
- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
UNE graphique bipartite est une dont sommets , V, peut être divisé en deux ensembles indépendants, V1 et V2, et chaque bord du graphique connecte un sommet en V1 à un sommet en V2 (Skiena 1990). Si chaque sommet de V1 est connecté à chaque sommet de V2 les graphique est appelé un complet graphique bipartite.
A côté de cela, un bipartite est-il un graphe ?
UNE le graphique est bipartite si et seulement si elle ne contient pas de cycle impair. UNE le graphique est bipartite si et seulement si elle est 2-colorable, (c'est-à-dire que son nombre chromatique est inférieur ou égal à 2). Le spectre d'un graphique est symétrique si et seulement si c'est un graphique bipartite.
Par la suite, la question est, un graphe bipartite peut-il être déconnecté ? 1 réponse. Si le sommet en haut à gauche était adjacent aux trois sommets de droite, vous auriez K3, 3, un graphique bipartite . Edit: Concernant votre question sur le nombre maximum d'arêtes a graphique bipartite sur n sommets pouvez avoir sans être connecté. Nous avons donc un sommet débranché.
Par rapport à cela, combien y a-t-il de graphes bipartis sur n sommets ?
La liste des connectés graphiques bipartites avec = 14 sommets est de 74 Mo compressé et nécessite quelques minutes pour être généré.
A quoi servent les graphes bipartites ?
Graphiques bipartites ont de nombreuses applications. Ils sont souvent habitué représentent des relations binaires entre deux types d'objets. Une relation binaire entre deux ensembles A et B est un sous-ensemble de A × B.
Conseillé:
Comment déterminer si une relation est une fonction sur un graphe ?

RÉPONSE : Exemple de réponse : Vous pouvez déterminer si chaque élément du domaine est associé à exactement un élément de la plage. Par exemple, si on vous donne un graphique, vous pouvez utiliser le test de la ligne verticale; si une ligne verticale coupe le graphique plus d'une fois, alors la relation que le graphique représente n'est pas une fonction
Qu'est-ce qu'un graphe de sélection directionnelle ?

Le graphique 1 montre la sélection directionnelle, dans laquelle un seul phénotype extrême est favorisé. Le graphique 2 illustre la sélection stabilisatrice, où le phénotype intermédiaire est favorisé par rapport aux traits extrêmes. Le graphique 3 montre une sélection disruptive, dans laquelle les phénotypes extrêmes sont favorisés par rapport aux intermédiaires
Qu'est-ce qu'un graphe d'une collection de paires ordonnées ?

Le graphe d'une relation est la collection de toutes les paires ordonnées de la relation. Ceux-ci sont généralement représentés par des points dans un système de coordonnées cartésiennes
Qu'est-ce qui rend un graphe quadratique ?

Le graphe d'une fonction quadratique est une parabole dont l'axe de symétrie est parallèle à l'axe des y. Les coefficients a,b et c dans l'équation y=ax2+bx+c y = a x 2 + b x + c contrôlent diverses facettes de l'apparence de la parabole lorsqu'elle est représentée graphiquement
Comment trouve-t-on le volume d'un cube avec une pyramide au sommet ?
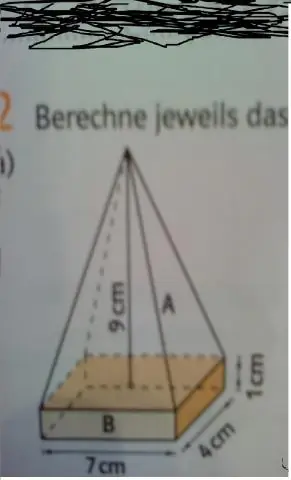
Pour trouver le volume de ce cube, multipliez la base par la largeur par la hauteur. Pour trouver le volume de la pyramide, prenez l'aire de la base, egin{align*}Bend{align*} et multipliez-la par la hauteur, puis multipliez-la par egin{align*}frac{1}{3}end{ aligner*}
