Table des matières:
Vidéo: Comment transformer des fonctions linéaires ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
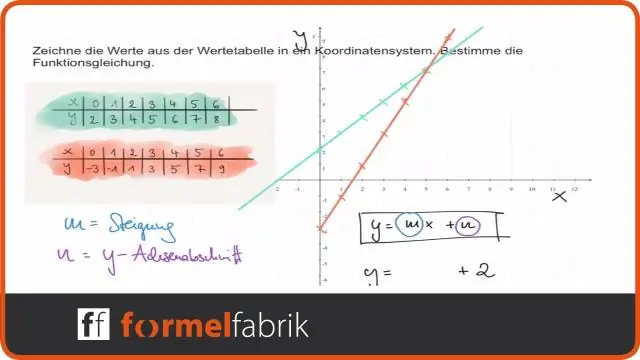
Comment: Étant donné l'équation d'un fonction linéaire , utilisation transformations pour représenter graphiquement le fonction linéaire sous la forme f(x)=mx+b f (x) = m x + b. Graphique f(x)=x f (x) = x. Étire ou compresse verticalement le graphique d'un facteur |m|. Déplacez le graphique vers le haut ou vers le bas de b unités.
Justement, comment décrivez-vous la transformation d'une fonction linéaire ?
Le graphique d'un fonction linéaire (une ligne) peut être déplacé autour de la grille de coordonnées. C'est ce qu'on appelle un transformation . Il y a trois bases transformations : translation (déplacement de la ligne), réflexion (inversion de la ligne) et mise à l'échelle (étirement de la ligne). Vous pouvez vous déplacer ( transformer ) la ligne verticalement ou horizontalement.
De plus, quelles transformations affectent la pente d'une fonction linéaire ? Transformer Fonctions linéaires (Étirement et compression) Les étirements et les compressions modifient la pente d'une fonction linéaire . Si la ligne devient plus raide, le fonction a été étiré verticalement ou comprimé horizontalement.
Par conséquent, comment transformer une fonction ?
Les règles de traduction/transformation de la fonction:
- f (x) + b décale la fonction b unités vers le haut.
- f (x) – b décale la fonction b unités vers le bas.
- f (x + b) décale la fonction b unités vers la gauche.
- f (x – b) décale la fonction b unités vers la droite.
- –f (x) reflète la fonction sur l'axe des x (c'est-à-dire à l'envers).
Comment refléter une fonction ?
UNE fonction peut être reflété autour d'un axe en multipliant par moins un. À réfléchir autour de l'axe des y, multipliez chaque x par -1 pour obtenir -x. À réfléchir autour de l'axe des x, multipliez f(x) par -1 pour obtenir -f(x).
Conseillé:
Qu'est-ce qu'une table de fonctions non linéaires ?
Une fonction non linéaire est une fonction qui n'est pas linéaire et le graphique d'une fonction linéaire est une ligne. Il est assez clair que le graphique de la fonction y = -x 2 + 4x n'est pas une ligne, donc la fonction est une fonction non linéaire
En quoi la résolution d'inéquations linéaires et d'équations linéaires sont-elles similaires ?
La résolution d'inéquations linéaires est très similaire à la résolution d'équations linéaires. La principale différence est que vous renversez le signe de l'inégalité lorsque vous divisez ou multipliez par un nombre négatif. La représentation graphique des inégalités linéaires présente quelques différences supplémentaires. La partie ombrée comprend les valeurs où l'inégalité linéaire est vraie
Toutes les fonctions linéaires ont-elles des inverses ?
Inverse des fonctions linéaires non constantes. Une fonction linéaire sera inversible tant qu'elle est non constante, ou en d'autres termes a une pente non nulle. Vous pouvez trouver l'inverse soit algébriquement, soit graphiquement en reflétant la ligne d'origine sur la diagonale y = x
A quoi servent les fonctions linéaires ?
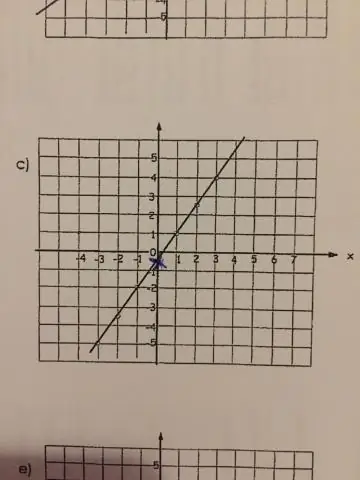
Une fonction linéaire est une fonction qui représente une ligne droite. Ce que cela signifie mathématiquement, c'est que la fonction a une ou deux variables sans exposant ni puissance. Si la fonction a plus de variables, les variables doivent être des constantes ou des variables connues pour que la fonction reste une fonction linéaire
Quels sont des exemples réels de fonctions linéaires ?
Réponse originale : Quelqu'un pourrait-il me donner un exemple de situation réelle de fonctions linéaires ? Les fonctions linéaires se produisent chaque fois que vous avez un taux de changement constant. Des exemples concrets sont : Trouver le courant consommé au jour 1,2,3… Vous louez une voiture. Vous conduisez une voiture à une vitesse de 60 km/h