- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
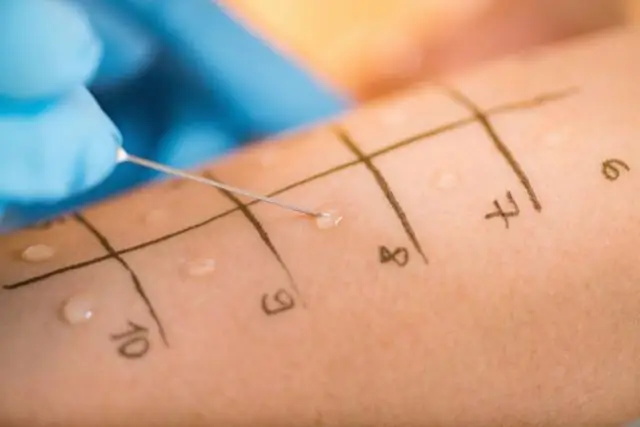
À- test est un type d'inférence statistique utilisée pour déterminer s'il existe une différence significative entre les moyennes de deux groupes, qui peut être liée dans certaines caractéristiques. Le t- test est l'un des nombreux tests utilisés à des fins d'hypothèse tests en statistiques . Calculer un t- test nécessite trois valeurs de données clés.
En conséquence, quel test statistique dois-je utiliser ?
Analyses statistiques avec SPSS
- Un échantillon de test t. Un test t à un échantillon nous permet de tester si une moyenne d'échantillon (d'une variable d'intervalle normalement distribuée) diffère significativement d'une valeur hypothétique.
- Test binomial.
- Qualité d'ajustement du chi carré.
- Test t sur deux échantillons indépendants.
- Test du chi carré.
- ANOVA à sens unique.
- Test de Kruskal Wallis.
- Test t apparié.
De plus, quels sont les 3 types de tests t ? Il existe trois principaux types de test t:
- Un test t pour échantillons indépendants compare les moyennes de deux groupes.
- Un test t pour échantillons appariés compare les moyennes du même groupe à différents moments (par exemple, à un an d'intervalle).
- Un test t à un échantillon teste la moyenne d'un seul groupe par rapport à une moyenne connue.
Les gens demandent aussi, que vous dit la statistique t ?
Les t -value mesure la taille de la différence par rapport à la variation de vos données d'échantillon. En d'autres termes, T est simplement la différence calculée représentée en unités d'erreur standard. Plus l'ampleur de T , plus la preuve contre l'hypothèse nulle est importante.
A quoi sert le test t de Student ?
Les t - test (aussi parfois appelé le Étudiant t - test ) est utilisé pour déterminer l'importance de la différence entre les moyennes de deux ensembles de données. En substance, le test compare la différence des moyennes par rapport aux variations aléatoires observées dans chaque ensemble.
Conseillé:
À quoi sert le test Northern blot?

Le Northern blot, ou RNA blot, est une technique utilisée dans la recherche en biologie moléculaire pour étudier l'expression des gènes par détection d'ARN (ou d'ARNm isolé) dans un échantillon
A quoi sert la solution de biotine histidine dans le test d'Ames ?

A quoi sert la solution biotine-histidine dans le test d'Ames ? La biotine sert de stimulateur de croissance bactérienne. L'histidine est utilisée pour permettre aux his-organismes de se développer, permettant ainsi aux cellules de subir une division cellulaire, ce qui est nécessaire pour que la mutation se produise
Qu'est-ce que les données non groupées dans les statistiques ?
Les données non groupées sont les données que vous collectez d'abord à partir d'une expérience ou d'une étude. Les données sont brutes, c'est-à-dire qu'elles ne sont pas triées en catégories, classées ou autrement regroupées. Un ensemble de données non groupé est essentiellement une liste de nombres
A quoi sert un test de complémentation ?

Essai de complémentation. Test de complémentation, également appelé test cis-trans, en génétique, test permettant de déterminer si deux mutations associées à un phénotype spécifique représentent deux formes différentes du même gène (allèles) ou sont des variations de deux gènes différents
A quoi sert le test d'Ames ?

Le test d'Ames est une méthode couramment utilisée qui utilise des bactéries pour tester si un produit chimique particulier peut provoquer des mutations dans l'ADN de l'organisme testé. Il s'agit d'un test biologique qui est formellement utilisé pour évaluer le potentiel mutagène de composés chimiques
