Table des matières:
Vidéo: Comment trouver l'angle d'un secteur dans un camembert ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
1 réponse
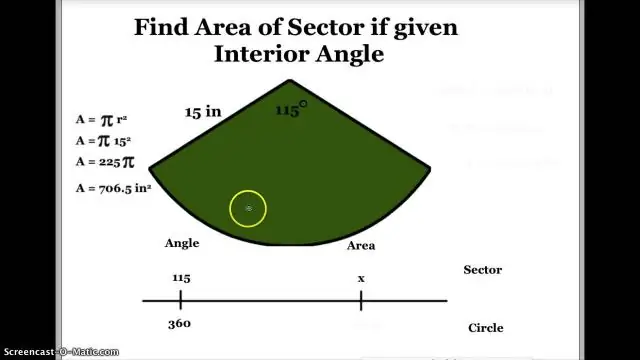
- Dans tous secteur , il y a 3 parties à considérer:
- La longueur de l'arc est une fraction de la circonférence. secteur la superficie est une fraction de la superficie totale. Les angle de secteur est une fraction de 360°
- Si la secteur est de 20 % de la diagramme circulaire , alors chacune de ces parties représente 20 % de l'ensemble.
- 20%×360°
- 20100×360=72°
De cette façon, comment trouve-t-on le degré d'un secteur de cercle ?
Explication: Si l'angle au centre mesure 60 degrés , divisez le total de 360 degrés dans le cercle par 60. Multipliez cela par la mesure de l'arc correspondant à trouve la circonférence totale du cercle . Utilisez la circonférence pour trouve theradius, puis utilisez le rayon pour trouve la zone.
Par la suite, la question est: qu'est-ce qu'un angle central dans un camembert ? Dans un diagramme circulaire , les différentes observations ou composants sont représentés par les secteurs d'un cercle et le cercle entier représente la somme des valeurs de tous les composants. angle au centre pour un composant est donnée par: Angle central pour un composant = Valeur du composantSomme des valeurs de tous les composants × 360°
De même, comment trouve-t-on le degré d'un pourcentage ?
Un cercle a 360 degrés , donc si vous voulez exprimer un angle en termes de pourcentage , il suffit de diviser la mesure de l'angle (en degrés ) par 360 et multiplier par 100. En sens inverse, diviser le pourcentage par 100 et multiplier par360.
Quelle est la formule pour trouver l'angle au centre ?
Formule pour S=rθ L'image ci-dessous illustre la relation entre le rayon et le angle au centre en radians. Le formule est S=rθ où s représente la longueur de l'arc, S=rθ représente la angle au centre en radians et r est la longueur du rayon.
Conseillé:
Comment trouve-t-on l'angle au centre étant donné l'aire et le rayon d'un secteur ?
Détermination de l'angle central à partir de l'aire du secteur (πr2) × (angle au centre en degrés 360 degrés) = aire du secteur. Si l'angle au centre est mesuré en radians, la formule devient à la place : aire du secteur = r2 × (angle au centre en radians ÷ 2). (θ ÷ 360 degrés) × πr2. (52,3 100π) × 360. (52,3 314) × 360
Comment trouver un compagnon perdu dans Fallout 4 ?
Le moyen le plus simple de localiser les compagnons Tout d'abord, c'est le moyen le plus simple de trouver des compagnons perdus ou des compagnons disparus. Si vous allez dans le menu de l'atelier lorsque vous êtes dans une colonie, rendez-vous sur Ressources> Divers, passez deux à travers, et vous rencontrerez la cloche
Comment trouve-t-on la longueur d'un secteur de cercle ?
Un angle au centre qui est sous-tendu par un arc majeur a une mesure supérieure à 180°. La formule de longueur d'arc est utilisée pour trouver la longueur d'un arc de cercle; l=rθ l = r θ, où θ est en radians. La zone du secteur se trouve A=12θr2 A = 1 2 θ r 2, où θ est en radians
Comment trouvez-vous la longueur de l'arc et la surface du secteur?
Un angle au centre qui est sous-tendu par un arc majeur a une mesure supérieure à 180°. La formule de longueur d'arc est utilisée pour trouver la longueur d'un arc de cercle; l=rθ l = r θ, où θ est en radians. La zone du secteur se trouve A=12θr2 A = 1 2 θ r 2, où θ est en radians
Comment trouver un angle au centre ?
Ainsi, l'angle central est essentiellement la longueur de l'arc multipliée par 360, les degrés d'un cercle complet, divisés par la circonférence du cercle. Comme vous pouvez le voir, la longueur de l'arc est simplement la circonférence d'un cercle (2πR) multipliée par le rapport de l'angle de l'arc à l'angle 360 complet d'un cercle