Table des matières:
Vidéo: Comment trouve-t-on l'angle au centre étant donné l'aire et le rayon d'un secteur ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2024-01-18 08:15
Détermination de l'angle central à partir de la zone du secteur
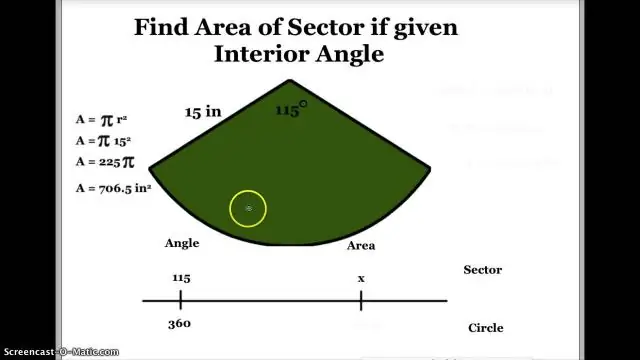
- (πr2) × ( angle au centre en degrés ÷ 360 degrés) = zone du secteur . Si la angle au centre est mesurée en radians, la formule devient à la place:
- zone du secteur = r2 × ( angle au centre en radians 2).
- (θ ÷ 360 degrés) × πr2.
- (52,3 100π) × 360.
- (52.3 ÷ 314) × 360.
De cette façon, comment trouve-t-on l'angle au centre étant donné le rayon ?
Trouve les Angle central de la longueur de l'arc et Rayon Vous pouvez également utiliser le rayon du cercle et la longueur de l'arc à trouve les angle au centre . Appelez la mesure de la angle au centre . Alors: θ = s ÷ r, où s est la longueur de l'arc et r est la rayon.
A côté de ci-dessus, comment trouve-t-on l'angle au centre d'un secteur ? Détermination de l'angle au centre Du Secteur Aire En d'autres termes: (πr2) × ( angle au centre en degrés ÷ 360 degrés) = secteur Région. Si la angle au centre se mesure en radians, le formule devient à la place: secteur aire = r2 × ( angle au centre en radians 2).
A côté de ci-dessus, quelle est l'aire d'un secteur ?
Les superficie d'un secteur en termes de L peut être obtenu en multipliant le total Région ou2 par le rapport de L au périmètre total 2πr.
Quelle est la formule de la circonférence ?
Pour calculer la circonférence d'un cercle , utilisez la formule C = πd, où "C" est la circonférence, "d" est le diamètre et π est 3,14. Si vous avez le rayon au lieu du diamètre, multipliez-le par 2 pour obtenir le diamètre. Vous pouvez également utiliser la formule de la circonférence d'un cercle en utilisant le rayon, qui est C = 2πr.
Conseillé:
Comment trouvez-vous la forme composante d'un vecteur étant donné la magnitude et l'angle?
VIDÉO En tenant compte de cela, 0 est-il un vecteur unitaire ? UNE vecteur unitaire est un vecteur qui a une magnitude de 1. La notation représente la norme, ou la magnitude, de vecteur v. La base vecteurs unitaires suis-je = (1, 0 ) et j = ( 0 , 1) qui sont de longueur 1 et ont des directions le long des axes x et y positifs respectivement.
Comment écris-tu une équation sous forme de pente de points étant donné deux points ?
Il existe différentes formes sous lesquelles on peut écrire l'équation d'une droite : la forme point-pente, la forme pente-intersection, la forme standard, etc. L'équation d'une droite étant donné deux points (x1, y1) et (x2, y2 ) par lequel passe la droite est donnée par, ((y - y1)/(x - x1)) / ((y2 - y1)/(x2 - x1))
Comment trouve-t-on l'équation d'une droite étant donné un point et une droite parallèle ?
L'équation de la droite sous la forme à l'origine de la pente est y=2x+5. La pente de la parallèle est la même : m=2. Ainsi, l'équation de la droite parallèle est y=2x+a. Pour trouver a, on utilise le fait que la droite doit passer par le point donné :5=(2)⋅(−3)+a
Comment trouver l'angle d'un secteur dans un camembert ?
1 réponse Dans n'importe quel secteur, il y a 3 parties à considérer : La longueur de l'arc est une fraction de la circonférence. La zone du secteur est une fraction de la zone entière. L'angle du secteur est une fraction de 360°. Si le secteur représente 20 % du camembert, alors chacune de ces parties représente 20 % de l'ensemble. 20%×360° 20100×360=72°
Comment trouve-t-on l'équation d'une hyperbole étant donné les asymptotes et les foyers ?
En utilisant le raisonnement ci-dessus, les équations des asymptotes sont y=±ab(x−h)+k y = ± a b (x &moins; h) + k. Comme les hyperboles centrées à l'origine, les hyperboles centrées en un point (h,k) ont des sommets, des co-sommets et des foyers qui sont liés par l'équation c2=a2+b2 c 2 = a 2 + b 2