Table des matières:
Vidéo: Comment utilisez-vous la règle de la main droite pour le produit croisé ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Les droit - règle de la main indique que l'orientation des vecteurs' produit croisé est déterminé en plaçant et queue à queue, en aplatissant le main droite , en l'étendant dans la direction de, puis en recourbant les doigts dans la direction que fait l'angle avec. Les pouce puis pointe dans la direction de.
Justement, comment faites-vous la règle de la main droite pour le produit croisé ?
Les produit croisé sera toujours un autre vecteur perpendiculaire aux deux vecteurs originaux. La direction de la produit croisé se trouve en utilisant le règle de droite , tandis que l'ampleur de la produit croisé est donné par: Le couple est la tendance d'une force à faire tourner un objet.
quelle est la règle du produit croisé ? Les produit croisé a × b est défini comme un vecteur c qui est perpendiculaire (orthogonal) à la fois à a et à b, avec une direction donnée par la main droite régner et une amplitude égale à l'aire du parallélogramme que le vecteur s'étend.
On peut aussi se demander, comment utilisez-vous la règle de la main droite ?
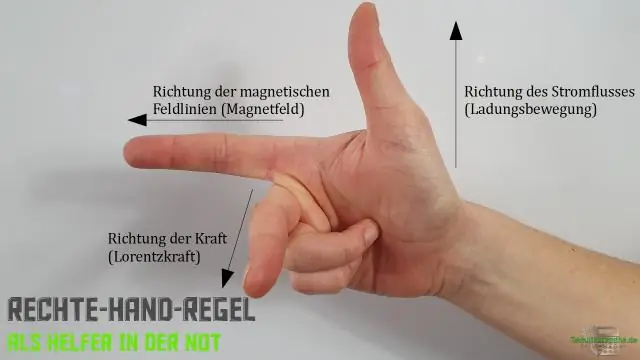
La direction du produit croisé peut être trouvée en appliquant la règle de la main droite comme suit:
- L'index pointe dans la direction du vecteur vitessev.
- Le majeur pointe dans la direction du vecteur de champ magnétique B.
- Le pouce pointe dans la direction du produit croisé F.
Comment calculez-vous le produit croisé ?
Nous pouvons calculer les Produit croisé de cette façon: Donc la longueur est: la longueur de a fois la longueur de b fois le sinus de l'angle entre a et b, puis on multiplie par le vecteur n pour s'assurer qu'il se dirige dans la bonne direction (à angle droit à la fois par a et b).
Conseillé:
Qu'est-ce qu'un produit croisé et scalaire ?
Produit scalaire, les interactions entre dimensions similaires (x*x, y*y, z*z) Produit croisé, les interactions entre différentes dimensions (x*y, y*z, z*x, etc.)
Quelle est la différence entre la règle du produit et la règle de la chaîne ?
Nous utilisons la règle de la chaîne pour différencier une « fonction d'une fonction », comme f(g(x)) en général. Nous utilisons la règle du produit pour différencier deux fonctions multipliées ensemble, comme f(x)g(x) en général. Mais notez que ce sont des fonctions distinctes : l'une ne dépend pas de la réponse de l'autre
Comment convertir la règle du quotient en règle du produit ?
La règle du quotient peut être considérée comme une application des règles du produit et de la chaîne. Si Q(x) = f(x)/g(x), alors Q(x) = f(x) * 1/(g(x)). Vous pouvez utiliser la règle du produit pour différencier Q(x), et le 1/(g(x)) peut être différencié en utilisant la règle de la chaîne avec u = g(x) et 1/(g(x)) = 1/u
Comment trouve-t-on l'équation d'une droite étant donné un point et une droite parallèle ?
L'équation de la droite sous la forme à l'origine de la pente est y=2x+5. La pente de la parallèle est la même : m=2. Ainsi, l'équation de la droite parallèle est y=2x+a. Pour trouver a, on utilise le fait que la droite doit passer par le point donné :5=(2)⋅(−3)+a
Serait-il logique de trouver l'équation d'une droite parallèle à une droite donnée et passant par un point sur la droite donnée ?
L'équation d'une droite parallèle ou perpendiculaire à une droite donnée ? Réponse possible : Les pentes des droites parallèles sont égales. Substituer la pente connue et les coordonnées d'un point sur l'autre ligne dans la forme point-pente pour trouver l'équation de la ligne parallèle