Vidéo: Quel est le sous-ensemble de l'espace échantillon ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
L'ensemble de tous les résultats possibles est appelé l'espace échantillon de l'expérience et est généralement désigné par S. Tout sous-ensemble E de l'espace échantillon S est appelé un événement. Voici quelques exemples. Exemple 1 Lancer une pièce.
À ce sujet, quel est un exemple d'espace d'échantillonnage ?
Les espace d'échantillon d'une expérience sont tous les résultats possibles de cette expérience. Quelques simples exemples : Les espacer pour le tirage au sort d'une pièce: {Pie, face.} Le espacer pour le lancer de dé: {1, 2, 3, 4, 5, 6.}
De plus, quelle est la différence entre l'espace événementiel et l'espace échantillon ? Il est parfois confondu avec le espace d'échantillon d'une expérience, désignée généralement par oméga(Ω), mais est différent : tandis que le espace d'échantillon d'une expérience contient tous les résultats possibles, le espace événementiel contient tous les ensembles de résultats; tous les sous-ensembles de espace d'échantillon.
Par la suite, la question est, quels sont les éléments d'un espace échantillon ?
Dans le cas d'un seul lancer, le espace d'échantillon a deux éléments qui, de façon interchangeable, peut être noté, disons, {Tête, Queue}, ou {H, T}, ou {0, 1}, Il y a six résultats possibles et le espace d'échantillon se compose de six éléments : {1, 2, 3, 4, 5, 6}.
Comment calculez-vous l'espace échantillon?
En utilisant le formule P = événement spécifique/ Espace d'échantillon , nous pouvons calculer les espace d'échantillon si on nous donne les valeurs (ou la capacité à atteindre) la probabilité et l'événement spécifique.
Conseillé:
Est-ce que p2 est un sous-espace de p3 ?
Oui! Puisque chaque polynôme de degré jusqu'à 2 est aussi un polynôme de degré jusqu'à 3, P2 est un sous-ensemble de P3. Et nous savons déjà que P2 est un espace vectoriel, c'est donc un sous-espace de P3. C'est-à-dire que R2 n'est pas un sous-ensemble de R3
Quelle est la différence entre les événements exhaustifs et l'espace échantillon ?
L'espace échantillon d'une expérience est l'ensemble de tous les résultats possibles. Si l'expérience lance un dé, l'espace échantillon est {1, 2, 3, 4, 5, 6}. Événements exhaustifs. Un ou plusieurs événements sont dits exhaustifs lorsqu'ils sont tels qu'au moins un des événements se produit obligatoirement
Quelle est la différence entre l'espace événementiel et l'espace échantillon ?
Il est parfois confondu avec l'espace échantillon d'une expérience, généralement désigné par omega(Ω), mais il est différent : alors que l'espace échantillon d'une expérience contient tous les résultats possibles, l'espace événement contient tous les ensembles de résultats; tous les sous-ensembles de l'espace échantillon
Lorsque le volume d'un échantillon de gaz est diminué la pression de l'échantillon de gaz ?
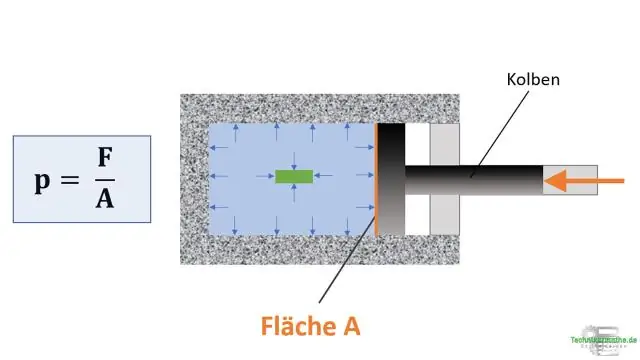
Diminution de la pression La loi des gaz combinés stipule que la pression d'un gaz est inversement proportionnelle au volume et directement liée à la température. Si la température est maintenue constante, l'équation est réduite à la loi de Boyle. Par conséquent, si vous diminuez la pression d'une quantité fixe de gaz, son volume augmentera
Comment trouvez-vous le nombre de résultats possibles dans un espace échantillon ?
Ensuite, multipliez le nombre de résultats par le nombre de rouleaux. Puisque nous ne roulons qu'une seule fois, le nombre de résultats possibles est de 6. La réponse est que l'espace d'échantillonnage est 1, 2, 3, 4, 5, 6 et le nombre de résultats possibles est de 6