Vidéo: Est-ce que p2 est un sous-espace de p3 ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Oui! Puisque tout polynôme de degré jusqu'à 2 est aussi un polynôme de degré jusqu'à 3, P2 est un sous-ensemble de P3 . Et nous savons déjà que P2 est un espace vectoriel, c'est donc un sous-espace de P3 . C'est-à-dire que R2 n'est pas un sous-ensemble de R3.
Les gens demandent aussi si l'ensemble de tous les polynômes de degré 3 est un sous-espace de p3 ?
1. P3 (F) est le espace vectoriel de tous les polynômes de degré ≦ 3 et avec des coefficients dans F. La dimension est 2 car 1 et x sont linéairement indépendants polynômes qui s'étend sur le sous-espace , et par conséquent ils sont une base pour cette sous-espace . (b) Soit U le sous-ensemble de P3 (F) consistant en tous les polynômes de degré 3.
qu'est-ce qu'un sous-espace de r3 ? A proprement parler, A Sous-espace est un espace vectoriel inclus dans un autre espace vectoriel plus grand. Par conséquent, toutes les propriétés d'un espace vectoriel, telles que la fermeture par addition et multiplication scalaire, restent vraies lorsqu'elles sont appliquées au Sous-espace . ex. Nous savons tous R3 est un espace vectoriel.
Les gens demandent aussi, qu'est-ce que p2 en algèbre linéaire ?
Laisser P2 être l'espace des polynômes de degré au plus 2, et définir le linéaire transformation T: P2 → R2 T(p(x)) = [p(0) p(1)] Par exemple T(x2 + 1) = [1 2].
Quel est le polynôme zéro ?
Zéro polynôme . La constante polynôme . dont les coefficients sont tous égaux à 0. Le polynôme fonction est la fonction constante de valeur 0, également appelée la zéro carte. Les zéro polynôme est l'identité additive du groupe additif de polynômes.
Conseillé:
Qu'est-ce que les sous-ensembles homogènes ?
Les tableaux des sous-ensembles homogènes indiquent quels groupes ont la même moyenne et lesquels ont une moyenne différente. Notez que le groupe de contrôle est dans le sous-ensemble 1 et les groupes mnémoniques A et B sont dans le sous-ensemble 2. Au sein d'un sous-ensemble, il n'y a pas de différence significative alors qu'entre les sous-ensembles il y a une différence significative
Qu'est-ce que le décapage sous vide ?
Résumé. Le procédé de stripping sous vide est utilisé pour la désodorisation des huiles blanchies neutres ainsi que pour le raffinage physique des huiles blanchies dégommées. Au cours du processus, l'huile chaude est exposée à un grand volume de fluide de décapage, ce qui provoque la vaporisation des constituants les plus volatils de l'huile
Qu'est-ce que l'extraction sous-critique au co2 ?
L'extraction au CO2 est un processus qui utilise du dioxyde de carbone sous pression pour extraire les composés phytochimiques souhaités (comme le chanvre) d'une plante. Vous pouvez également effectuer des extractions de CO2 sous-critiques et des extractions « moyennes critiques », une plage générale entre sous-critique et supercritique
Est-ce que ça va de faire pipi sous la douche ?
Faire pipi sous la douche est hygiénique et bon pour l'environnement. Et pour cause, faire pipi sous la douche n'est vraiment pas aussi dégoûtant qu'on le prétend. Pour commencer, c'est plus hygiénique que de faire pipi dans les toilettes, ce qui entraîne une quantité importante d'éclaboussures - sur votre jean, sur vos mains et même sur votre visage
Comment écrivez-vous sous forme de fraction sous la forme la plus simple ?
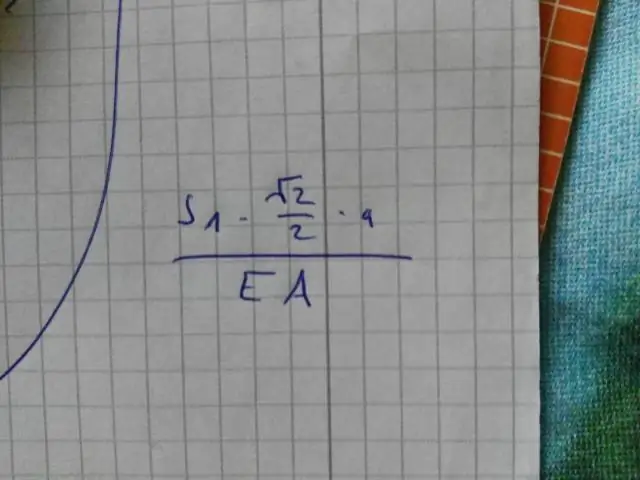
Lors de l'écriture des fractions sous la forme la plus simple, il y a deux règles à suivre : Demandez si le numérateur et le dénominateur peuvent être divisés par le même nombre, qui est appelé un facteur commun. Voir si au moins un nombre dans la fraction est un nombre premier