Vidéo: Qu'est-ce qu'un exemple d'énoncé biconditionnel en géométrie ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Les déclaration r s est vrai par définition d'un conditionnel. Les déclaration s r est également vrai. Par conséquent, la phrase "Un triangle est isocèle si et seulement s'il a deux côtés congrus (égaux)" est biconditionnel . Résumé: Un déclaration biconditionnelle est défini comme vrai chaque fois que les deux parties ont la même valeur de vérité.
De plus, qu'est-ce qu'un exemple d'énoncé biconditionnel ?
Exemples de déclarations biconditionnelles Les déclarations biconditionnelles car ces deux ensembles seraient: Le polygone n'a que quatre côtés si et seulement si le polygone est un quadrilatère. Le polygone est un quadrilatère si et seulement si le polygone n'a que quatre côtés.
De plus, qu'est-ce qu'un biconditionnel en géométrie ? UNE biconditionnel L'instruction est une combinaison d'une instruction conditionnelle et de sa réciproque écrite sous la forme si et seulement si. Deux segments de droite sont congrus si et seulement s'ils sont de longueur égale. UNE biconditionnel est vrai si et seulement si les deux conditions sont vraies.
À ce sujet, quand pouvez-vous écrire une déclaration biconditionnelle ?
' Déclarations biconditionnelles sont vrai déclarations qui combinent l'hypothèse et la conclusion avec les mots clés « si et seulement si ». ' Par exemple, le déclaration sera prendre cette forme: (hypothèse) si et seulement si (conclusion). Nous pourrions aussi écrivez ainsi: (conclusion) si et seulement si (hypothèse).
Que signifie IFF dans une déclaration biconditionnelle ?
En logique et en mathématiques, la logique biconditionnel , parfois appelé matériau biconditionnel , est le connecteur logique utilisé pour joindre deux déclarations et pour former le déclaration " si et seulement si ", où est dit l'antécédent, et le conséquent. Ceci est souvent abrégé en " si ssi ".
Conseillé:
Qu'est-ce qu'un énoncé biconditionnel en logique?
Lorsque nous combinons deux instructions conditionnelles de cette façon, nous avons un biconditionnel. Définition : Une déclaration biconditionnelle est définie comme vraie chaque fois que les deux parties ont la même valeur de vérité. Le biconditionnel p q représente « p si et seulement si q », où p est une hypothèse et q est une conclusion
Qu'est-ce qu'un énoncé de thèse pour les collégiens ?
Qu'est-ce qu'une déclaration de thèse? Un énoncé de thèse est une à deux phrases dans l'introduction d'un essai que l'écrivain utilise pour « préparer le terrain » pour le lecteur. L'énoncé de la thèse fournit le point de mire pour l'écriture qui suit et permet au lecteur de savoir sur quoi portera l'essai
Qu'est-ce qu'un exemple d'énoncé de thèse ?
Un énoncé de thèse est une phrase qui exprime l'idée principale d'un document de recherche ou d'un essai, comme un essai explicatif ou un essai argumentatif. Il fait une réclamation, répond directement à une question. En règle générale, votre énoncé de thèse peut être la dernière ligne du premier paragraphe de votre document de recherche ou dissertation
Qu'est-ce que l'énoncé de la thèse dans une histoire?
Définition. Dans tout essai, l'énoncé de la thèse établit le but de l'essai pour le lecteur. Une bonne thèse correspond à la durée du devoir, fait une déclaration sur votre point global et inclut les points spécifiques que vous donnerez pour soutenir cette idée de l'histoire
Comment écrivez-vous un biconditionnel comme deux conditionnels?
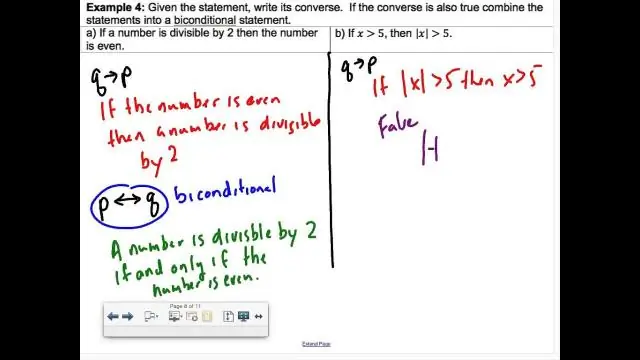
Il s'agit d'une combinaison de deux instructions conditionnelles, "si deux segments de ligne sont congrus alors ils sont de longueur égale" et "si deux segments de ligne sont de longueur égale alors ils sont congrus". Un biconditionnel est vrai si et seulement si les deux conditions sont vraies. Les bi-conditionnels sont représentés par le symbole ↔ ou ⇔