Vidéo: Comment écrivez-vous un biconditionnel comme deux conditionnels?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
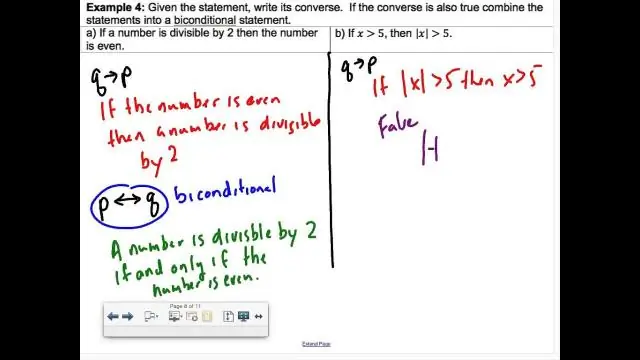
C'est une combinaison de deux conditionnels déclarations, « si deux les segments de droite sont congrus alors ils sont de longueur égale » et « si deux les segments de ligne sont de longueur égale alors ils sont congrus ». UNE biconditionnel est vrai si et seulement si les deux conditionnels sont vrai. Bi- conditionnels sont représentés par le symbole ↔ ou ⇔.
De plus, quand pouvez-vous écrire une déclaration biconditionnelle ?
Lorsque tu combiner un conditionnel déclaration et sa réciproque, tu créer un déclaration biconditionnelle . UNE déclaration biconditionnelle est un déclaration cette pouvez s'écrit sous la forme « p si et seulement si q ». Cela signifie « si p, alors q » et « si q, alors p. » Les biconditionnel "p si et seulement si q" pouvez aussi être écrit comme « p iff q » ou p ? q.
De plus, est-ce seulement si un biconditionnel? SI ET SEULEMENT SI , est un biconditionnel déclaration, ce qui signifie que les deux déclarations sont vraies ou les deux sont fausses. C'est donc essentiellement et SI ” déclaration qui fonctionne dans les deux sens.
A savoir aussi, qu'est-ce que les déclarations conditionnelles et biconditionnelles ?
Quand on combine deux expressions conditionnelles de cette façon, nous avons un biconditionnel . Définition: A déclaration biconditionnelle est défini comme vrai chaque fois que les deux parties ont la même valeur de vérité. Dans la table de vérité ci-dessus, p q est vrai lorsque p et q ont les mêmes valeurs de vérité (c'est-à-dire lorsque les deux sont vrais ou les deux sont faux.)
Quel est un exemple d'énoncé biconditionnel ?
Exemples de déclarations biconditionnelles Les déclarations biconditionnelles car ces deux ensembles seraient: Le polygone n'a que quatre côtés si et seulement si le polygone est un quadrilatère. Le polygone est un quadrilatère si et seulement si le polygone n'a que quatre côtés.
Conseillé:
Qu'est-ce qu'un énoncé biconditionnel en logique?
Lorsque nous combinons deux instructions conditionnelles de cette façon, nous avons un biconditionnel. Définition : Une déclaration biconditionnelle est définie comme vraie chaque fois que les deux parties ont la même valeur de vérité. Le biconditionnel p q représente « p si et seulement si q », où p est une hypothèse et q est une conclusion
Pourquoi les moisissures aquatiques sont-elles décrites comme des champignons comme les protistes ?
Le deuxième groupe de protistes ressemblant à des champignons est celui des moisissures aquatiques. Les moisissures aquatiques sont des protistes filamenteux, ce qui signifie que leurs cellules forment de longues structures en forme de brins. Ces filaments ressemblent à la croissance de certains champignons, et ils peuvent également former des spores comme des champignons. Donc, encore une fois, cela explique la partie moule du nom
Pourquoi la déchirure du papier et la brûlure du papier sont-elles considérées comme deux types de changements ?
La déchirure d'un papier est un changement physique car lorsque le papier est déchiré, seule l'apparence du papier est modifiée et aucune nouvelle substance ne se forme. la déchirure du papier est un changement physique car il reste le même mais la combustion du papier est un changement chimique car il se transforme en cendres
Deux composés peuvent-ils être utilisés comme réactifs pour la réaction de synthèse ?
7. Deux éléments peuvent-ils être utilisés comme réactifs pour une réaction de synthèse ? Si oui, donnez au moins un exemple du modèle 1 pour étayer votre réponse. Les éléments et les composés peuvent être vus dans les produits des réactions de décomposition
Quels sont les deux objets utilisés comme bougie standard ?
Les bougies standard les plus couramment utilisées en astronomie sont les étoiles variables Céphéides et les étoiles RR Lyrae. Dans les deux cas, la magnitude absolue de l'étoile peut être déterminée à partir de sa période de variabilité