
- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
Depuis un point d'intersection est sur les deux lignes, il doit être une solution aux deux équations. 5. Joël dit un système de linéaire équations aura toujours exactement une solution chaque fois que les pentes des deux droites sommes différent. Par conséquent, ils doivent couper à une et seulement un point.
Compte tenu de cela, peut-il y avoir plus d'un point d'intersection?
Explication: Si vous avez des pentes différentes à un point les lignes volonté se croisent car ils ne sont pas parallèles. Donc pour leur être plusieurs points d'intersection non seulement la pente doit être la même, mais l'ordonnée à l'origine doit l'être également.
peut-il y avoir plus d'un point d'intersection entre les graphiques de deux équations linéaires expliquer? À moins que le graphiques de deux équations linéaires coïncider, il peut être seulement un point d'intersection , car deux lignes peut se croiser au plus un point.
A cela, combien y a-t-il de solutions lorsque les droites se coupent en un seul point ?
Les les lignes se coupent en un point , donc les deux lignes ont un seul point en commun. Là est une seule solution au système. Parce que le lignes ne sont pas les mêmes, les équations sont indépendantes. Parce que là est une seule solution , ce système est cohérent.
Comment trouvez-vous les points d'intersection?
Pour trouver le point d'intersection algébriquement, résolvez chaque équation pour y, définissez les deux expressions pour y égales l'une à l'autre, résolvez pour x et branchez la valeur de x dans l'une des équations d'origine pour trouver la valeur y correspondante. Les valeurs de x et y sont les valeurs x et y du point d'intersection.
Conseillé:
La fonction est-elle linéaire ou non linéaire ?

Une fonction linéaire est une fonction de forme standard y = mx + b, où m est la pente et b l'ordonnée à l'origine, et dont le graphique ressemble à une ligne droite. Il existe d'autres fonctions dont le graphique n'est pas une ligne droite. Ces fonctions sont appelées fonctions non linéaires et se présentent sous de nombreuses formes différentes
Peut-il y avoir plus d'un point d'intersection entre les graphiques de deux équations linéaires ?

À moins que les graphiques de deux équations linéaires ne coïncident, il ne peut y avoir qu'un seul point d'intersection, car deux droites peuvent se croiser en au plus un point. A partir de ce point, déplacez une unité vers la droite et déplacez verticalement la valeur de la pente pour tracer un deuxième point. Reliez ensuite les deux points
Quelle est la différence entre le système impérial et le système métrique ?

La plupart des pays utilisent le système métrique, qui utilise les unités de mesure telles que les mètres et les grammes et ajoute des préfixes tels que kilo, milli et centi pour compter les ordres de grandeur. Aux États-Unis, nous utilisons l'ancien système impérial, où les choses sont mesurées en pieds, pouces et livres
Comment savoir si une équation est linéaire ou non linéaire ?

Utilisation d'une équation Simplifiez l'équation aussi étroitement que possible sous la forme y = mx + b. Vérifiez si votre équation a des exposants. S'il a des exposants, il est non linéaire. Si votre équation n'a pas d'exposant, elle est linéaire
Pourquoi l'eau a-t-elle un point d'ébullition et un point de fusion élevés ?
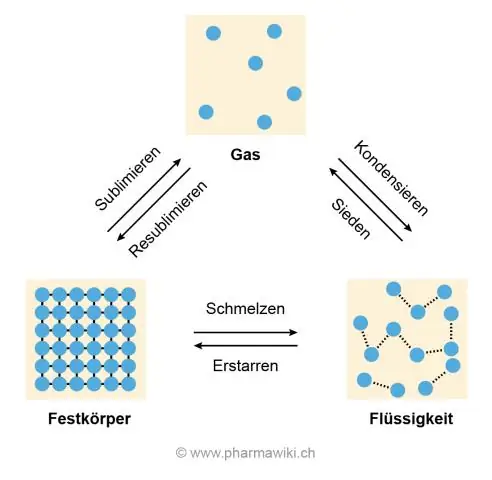
La raison des températures de fusion et d'ébullition élevées est la liaison hydrogène entre les molécules d'eau qui les oblige à se coller les unes aux autres et à résister à la séparation, ce qui se produit lorsque la glace fond et que l'eau bout pour devenir un gaz
