
- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
Les chi - la distribution carrée est obtenu comme la somme des carrés de k variables aléatoires gaussiennes indépendantes, à moyenne nulle et à variance unitaire. Généralisations de cette la distribution peut être obtenu en additionnant les carrés d'autres types de variables aléatoires gaussiennes.
De plus, quel est l'écart type de la distribution du Chi carré ?
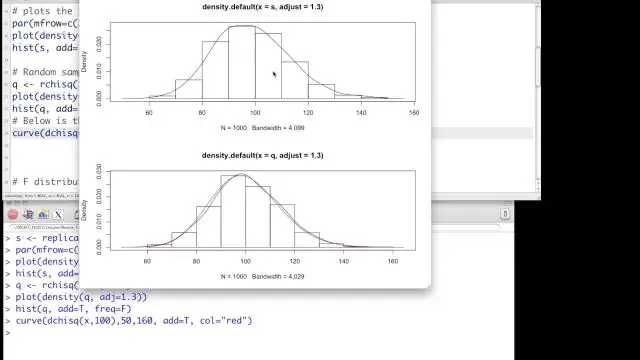
Lorsque df > 90, le chi - carré courbe se rapproche de la distribution normale . Pour X∼χ21, 000 X ∼ χ 1, 000 2 la moyenne, Μ=df=1, 000 Μ = d f = 1, 000 et le écart-type , =√2(1, 000) σ = 2 (1, 000).
qu'est-ce que la distribution chi carré avec des exemples? Les Chi - Distribution carrée Les distribution du chi carré est le Distribution de la somme de ces aléatoires échantillons au carré . Les degrés de liberté (k) sont égaux au nombre de échantillons étant sommée. Pour Exemple , si vous avez pris 10 échantillons de la normale Distribution , alors df = 10.
Le Chi carré est-il normalement distribué ?
La moyenne d'un Répartition du Chi carré est ses degrés de liberté. Place du Chi les distributions sont positivement asymétriques, le degré d'asymétrie diminuant avec l'augmentation des degrés de liberté. Au fur et à mesure que les degrés de liberté augmentent, le Répartition du Chi carré s'approche d'un distribution normale.
Que nous dit Chi Square ?
Les Chi - carré test est destiné à tester la probabilité qu'une distribution observée soit due au hasard. Elle est également appelée statistique de « qualité de l'ajustement », car elle mesure dans quelle mesure la distribution observée des données correspond à la distribution attendue si les variables sont indépendantes.
Conseillé:
Quelle est la différence entre la corrélation et le chi carré ?
Ainsi, la corrélation concerne la relation linéaire entre deux variables. Habituellement, les deux sont continus (ou presque), mais il existe des variations pour le cas où l'un est dichotomique. Le chi carré concerne généralement l'indépendance de deux variables. Habituellement, les deux sont catégoriques
Le chi carré peut-il être négatif ?
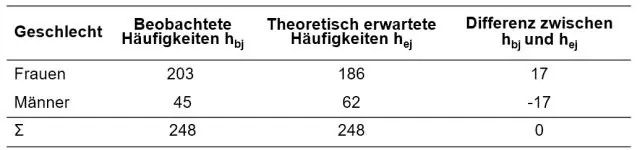
Voulez-vous dire : les valeurs du chi carré peuvent-elles être négatives ? La réponse est non. La valeur d'un chi carré ne peut pas être négative car elle est basée sur une somme de différences au carré (entre les résultats obtenus et attendus)
Le sin au carré x est-il égal à sin x au carré ?
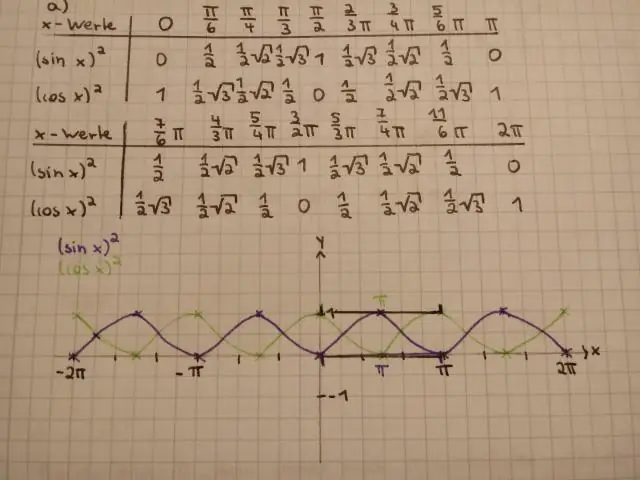
Oui c'est le cas. sin^2x est le même assinx^2 car dans les deux cas, le '^2' se rapporte uniquement au x
Quelle est la moyenne de la distribution du chi carré ?

La distribution du Chi carré est la distribution de la somme des écarts normaux standard au carré. Les degrés de liberté de la distribution sont égaux au nombre d'écarts normaux standard additionnés. La moyenne d'une distribution du Chi carré est ses degrés de liberté
Comment calcule-t-on la distribution du chi carré ?

Distribution du Khi deux La moyenne de la distribution est égale au nombre de degrés de liberté : μ = v. La variance est égale à deux fois le nombre de degrés de liberté : σ2 = 2 * v. Lorsque les degrés de liberté sont supérieurs supérieur ou égal à 2, la valeur maximale de Y se produit lorsque Χ2 = v - 2
