Vidéo: Qu'est-ce que la loi d'identité en mathématiques discrètes ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Alors le droit de l'identité , p∧T≡p, signifie que la conjonction de toute phrase p avec une tautologie arbitraire T aura toujours la même valeur de vérité que p (c'est-à-dire qu'elle sera logiquement équivalente à p). Cela signifie que la disjonction de toute phrase p avec une tautologie arbitraire T sera toujours vraie (sera elle-même une tautologie).
A savoir aussi, quelle est la loi d'identité en maths ?
Un identité est une égalité qui est vraie quelles que soient les valeurs choisies pour ses variables. Par exemple, le identité (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 est vrai pour tous les choix de x et y, qu'il s'agisse de nombres réels ou complexes.
Par ailleurs, qu'est-ce qu'un exemple de principe d'identité ? En logique, la loi de identité affirme que chaque chose est identique à elle-même. C'est la première des trois lois de la pensée, avec la loi de non-contradiction et la loi du tiers exclu. Il peut également être écrit de manière moins formelle car A est A. Une déclaration d'un tel principe est "La rose est une rose est une rose est une rose."
Par la suite, on peut aussi se demander, qu'est-ce que la loi de De Morgan en mathématiques discrètes ?
Les lois de De Morgan décrire comment mathématique les énoncés et les concepts sont liés par leurs opposés. En théorie des ensembles, Les lois de De Morgan relier l'intersection et l'union d'ensembles par des compléments. En logique propositionnelle, Les lois de De Morgan relier les conjonctions et les disjonctions de propositions par la négation.
Qu'est-ce que les implications mathématiques discrètes?
Définition: Soient p et q des propositions. La proposition "p ou q" notée p q, est fausse lorsque p et q sont fausses et est vraie sinon. La proposition "p implique q" notée p → q est appelée implication . Il est faux lorsque p est vrai et q est faux et est vrai sinon.
Conseillé:
Pourquoi la loi de Dalton est une loi limitative ?
Limitation de la loi de Dalton La loi est valable pour les gaz réels à basse pression, mais à haute pression, elle s'écarte considérablement. Le mélange de gaz est de nature non réactive. On suppose également que l'interaction entre les molécules de chaque gaz individuel est la même que les molécules dans le mélange
Qu'est-ce que les matrices en mathématiques discrètes?
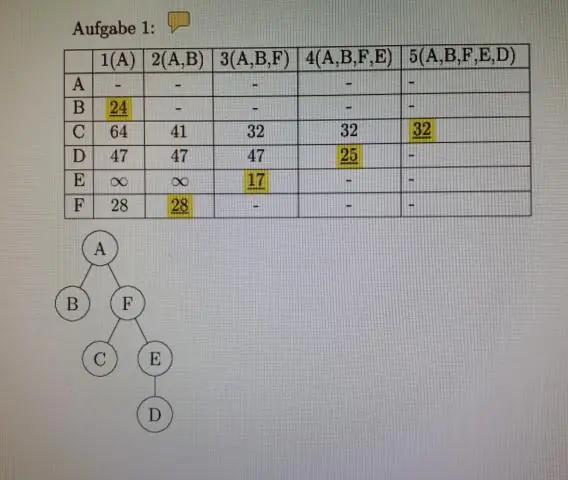
Les Mathématiques Discrètes Et Ses Applications Chapitre 2 Notes 2.6 Matrices Présentations Diapositives Par Adil Aslammailto:[email protected]. Définition de la matrice • Une matrice est un tableau rectangulaire de nombres. Une matrice avec m lignes et n colonnes est appelée une matrice m x n. Le pluriel de matrice est matrices
Qu'est-ce que l'équivalence en mathématiques discrètes ?
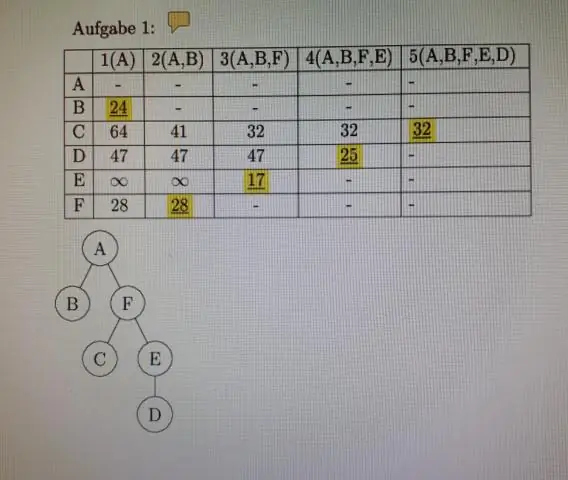
En mathématiques, une relation d'équivalence est une relation binaire qui est réflexive, symétrique et transitive. La relation 'est égal à' est l'exemple canonique d'une relation d'équivalence, où pour tout objet a, b et c : a = a (propriété réflexive), si a = b et b = c alors a = c (propriété transitive )
Quelle est la différence entre une loi sociétale et une loi scientifique ?
Lois de société. Les lois scientifiques sont fondées sur des preuves scientifiques étayées par l'expérimentation. Exemples de lois scientifiques. Les lois sociétales sont basées sur le comportement et la conduite de la société ou du gouvernement
Qu'est-ce que les mathématiques discrètes définies ?
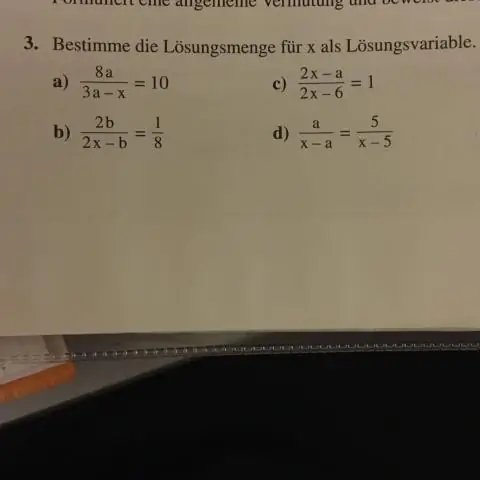
Un ensemble est une collection non ordonnée de différents éléments. Un ensemble peut être écrit explicitement en listant ses éléments à l'aide de set bracket. Si l'ordre des éléments est modifié ou si un élément d'un ensemble est répété, cela n'apporte aucun changement à l'ensemble