- Auteur Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
Dans mathématiques , un équivalence relation est une relation binaire qui est réflexive, symétrique et transitive. La relation "est égal à" est l'exemple canonique d'un équivalence relation, où pour tous les objets a, b et c: a = a (propriété réflexive), si a = b et b = c alors a = c (propriété transitive).
D'ailleurs, qu'est-ce que l'équivalence en maths ?
Équivalent signifie égal en valeur, en fonction ou en signification. Dans math , équivalent les nombres sont des nombres qui s'écrivent différemment mais représentent le même montant.
qu'est-ce que la loi d'identité en mathématiques discrètes ? Alors le droit de l'identité , p∧T≡p, signifie que la conjonction de toute phrase p avec une tautologie arbitraire T aura toujours la même valeur de vérité que p (c'est-à-dire qu'elle sera logiquement équivalente à p). Cela signifie que la disjonction de toute phrase p avec une tautologie arbitraire T sera toujours vraie (sera elle-même une tautologie).
De plus, qu'est-ce qu'un exemple de relation d'équivalence?
Un relation d'équivalence sur un ensemble S, est un relation sur S qui est réflexif, symétrique et transitif. Exemples : Soit S = ℤ et définissons R = {(x, y) | x et y ont la même parité} c'est-à-dire que x et y sont soit tous les deux pairs, soit tous les deux impairs. La parité relation est un relation d'équivalence.
Quelle est la loi de l'équivalence logique ?
Dans logique et les mathématiques, les énoncés et sont dits logiquement équivalent , s'ils sont démontrables les uns des autres sous un ensemble d'axiomes, ou ont la même valeur de vérité dans chaque modèle. Les équivalence logique de et est parfois exprimé par,, ou., selon la notation utilisée.
Conseillé:
Qu'est-ce que la loi d'identité en mathématiques discrètes ?

Ainsi, la loi d'identité, p&et;T≡p, signifie que la conjonction de toute phrase p avec une tautologie arbitraire T aura toujours la même valeur de vérité que p (c'est-à-dire qu'elle sera logiquement équivalente à p). Cela signifie que la disjonction de toute phrase p avec une tautologie arbitraire T sera toujours vraie (sera elle-même une tautologie)
Qu'est-ce que les matrices en mathématiques discrètes?
Les Mathématiques Discrètes Et Ses Applications Chapitre 2 Notes 2.6 Matrices Présentations Diapositives Par Adil Aslammailto:adilaslam5959@gmail.com. Définition de la matrice • Une matrice est un tableau rectangulaire de nombres. Une matrice avec m lignes et n colonnes est appelée une matrice m x n. Le pluriel de matrice est matrices
Qu'est-ce que les mathématiques discrètes définies ?
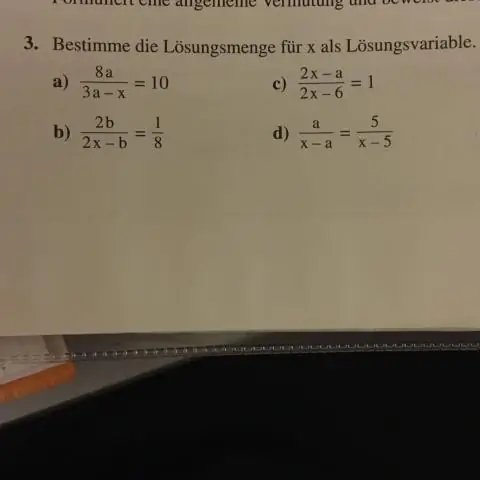
Un ensemble est une collection non ordonnée de différents éléments. Un ensemble peut être écrit explicitement en listant ses éléments à l'aide de set bracket. Si l'ordre des éléments est modifié ou si un élément d'un ensemble est répété, cela n'apporte aucun changement à l'ensemble
Quelle est la définition des données discrètes ?

Définition des données discrètes : informations pouvant être classées dans une classification. Les données discrètes sont basées sur des comptages. Seul un nombre fini de valeurs est possible, et les valeurs ne peuvent pas être subdivisées de manière significative. Ce sont généralement des choses comptées en nombres entiers
Comment trouver le pH au point d'équivalence d'un acide fort et d'une base forte ?

Au point d'équivalence, des quantités égales d'ions H+ et OH- se combinent pour former H2O, ce qui donne un pH de 7,0 (neutre). Le pH au point d'équivalence pour ce titrage sera toujours de 7,0, notez que cela n'est vrai que pour les titrages d'acide fort avec une base forte
