Table des matières:
Vidéo: Comment prouver qu'une matrice est un sous-espace ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Le centralisateur d'un Matrix est un sous-espace Soit V le espace vectoriel de n×n matrices , et M∈V a fixe matrice . Définir W={A∈V∣AM=MA}. L'ensemble W est appelé ici le centralisateur de M dans V. Prouver que W est un sous-espace de V.
Ici, comment prouvez-vous un sous-espace?
Pour montrer qu'un sous-ensemble est un sous-espace, vous devez montrer trois choses:
- Montrer qu'il est fermé sous ajout.
- Montrer qu'il est fermé par multiplication scalaire.
- Montrer que le vecteur 0 est dans le sous-ensemble.
De plus, qu'est-ce qu'une base d'une matrice ? Quand on cherche le base du noyau d'un matrice , nous supprimons tous les vecteurs colonnes redondants du noyau et gardons les vecteurs colonnes linéairement indépendants. Par conséquent, un base est juste une combinaison de tous les vecteurs linéairement indépendants.
Sachez également que la matrice identité est un sous-espace ?
En particulier, le matrice d'identité en soi (1 sur la diagonale principale, 0 ailleurs) n'est pas un sous-espace de la collection de 2×2 matrices , car si le matrice d'identité je suis dans le sous-espace , alors cI doit être dans le sous-espace pour tous les nombres c.
Qu'est-ce qu'un sous-espace d'une matrice ?
UNE sous-espace est un espace vectoriel contenu dans un autre espace vectoriel. Alors chaque sous-espace est un espace vectoriel à part entière, mais il est également défini par rapport à un autre espace vectoriel (plus grand).
Conseillé:
Comment prouver que quelque chose est une base ?
VIDÉO Également demandé, qu'est-ce qui fait une base? En mathématiques, un ensemble B d'éléments (vecteurs) dans un espace vectoriel V est appelé un base , si chaque élément de V peut être écrit d'une manière unique comme une combinaison linéaire (finie) d'éléments de B.
Comment transformer une matrice en matrice d'identité ?
VIDÉO De plus, comment trouve-t-on l'inverse d'une matrice à l'aide d'une matrice identité ? Cela fonctionne de la même manière pour matrices . Si vous multipliez un matrice (comme A) et ses inverse (dans ce cas, A – 1 ), vous obtenez le matrice d'identité I.
Comment écrivez-vous sous forme de fraction sous la forme la plus simple ?
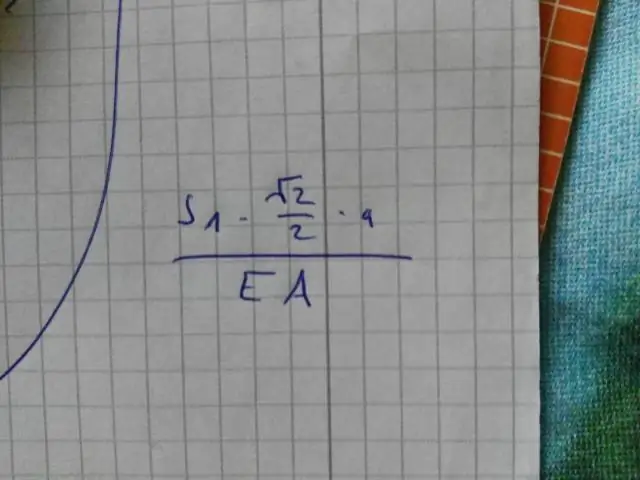
Lors de l'écriture des fractions sous la forme la plus simple, il y a deux règles à suivre : Demandez si le numérateur et le dénominateur peuvent être divisés par le même nombre, qui est appelé un facteur commun. Voir si au moins un nombre dans la fraction est un nombre premier
Comment prouver que la lumière est une particule ?
L'effet photoélectrique se produit lorsqu'un photon de haute énergie (particule lumineuse) frappe une surface métallique et qu'un électron est éjecté tandis que le photon disparaît. Cela montre que la lumière peut être une particule ET une onde. Pour concevoir une expérience montrant que la lumière est une particule, vous pouvez vous référer à l'expérience Electron Double Slit
Comment écrivez-vous une équation sous forme d'interception de pente pour une table?
Prenez l'équation y = mx + b et insérez la valeur m (m = 1) et une paire de coordonnées (x, y) du tableau, telles que (5, 3). Ensuite, résolvez pour b. Enfin, utilisez les valeurs m et b que vous avez trouvées (m = 1 et b = -2) pour écrire l'équation