- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
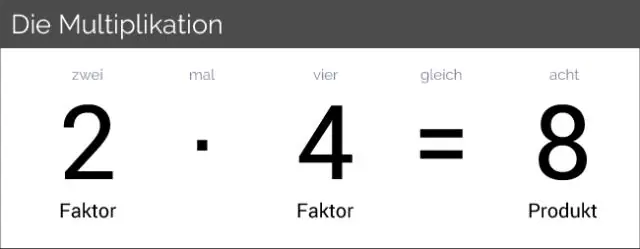
Propriété d'identité de la multiplication : Le produit de 1 et de n'importe quel nombre est ce nombre. Pour Exemple , 7 × 1 = 7 7 fois 1 = 7 7×1=77, fois, 1, égal, 7.
Justement, quel est un exemple de propriété d'identité ?
À propos de la transcription. Les propriété d'identité de 1 dit que tout nombre multiplié par 1 garde son identité . En d'autres termes, tout nombre multiplié par 1 reste le même. La raison pour laquelle le nombre reste le même est que multiplier par 1 signifie que nous avons 1 copie du nombre. Pour Exemple , 32x1=32.
De même, quelles sont les propriétés de la multiplication et des exemples ? Il y a quatre propriétés impliquant la multiplication qui aideront à faire problèmes plus facile à résoudre. Ils sont les commutatif , associatif , multiplicatif identité et les propriétés distributives. Propriété d'identité multiplicative : Le produit de n'importe quel nombre et un est ce nombre. Par exemple 5 * 1 = 5.
Par conséquent, quelle est la propriété d'identité de la multiplication ?
Les propriété d'identité car l'addition nous dit que zéro ajouté à n'importe quel nombre est le nombre lui-même. Zéro est appelé "l'additif identité ." Les propriété d'identité pour multiplication nous dit que le nombre 1 multiplié par n'importe quel nombre donne le nombre lui-même. Le nombre 1 est appelé le "multiplicatif identité ." Une addition.
Quel est un exemple de propriété commutative?
Un Exemple est 8+2=10 2+8=10. Les définition de la propriété commutative d'addition est, lorsque nous substituons n'importe quel nombre pour a et b pour Exemple ,. Pour Exemple ,, parce que et sont les deux. Peu importe que le ou le vienne en premier. 2+3=3+2 est identique à, quand et.
Conseillé:
Qu'est-ce qu'un non exemple de propriété commutative de multiplication ?
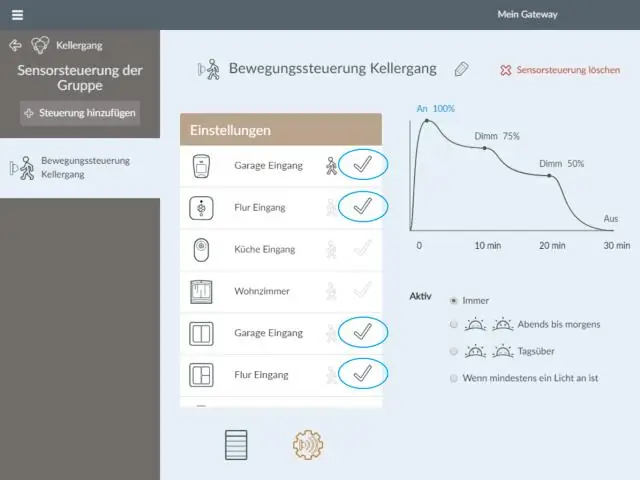
Soustraction (non commutative) De plus, la division, les compositions de fonctions et la multiplication matricielle sont deux exemples bien connus qui ne sont pas commutatifs
La charge électrique est-elle une propriété de l'électricité uniquement ou la charge est-elle une propriété de tous les atomes ?

Une charge positive attire une charge négative et repousse les autres charges positives. La charge électrique est-elle une propriété de l'électricité uniquement ou la charge est-elle une propriété de tous les atomes ? La charge électrique est une propriété de tous les atomes
Quelle est la définition de la propriété associative dans la multiplication?

Définition : La propriété associative indique que vous pouvez ajouter ou multiplier quelle que soit la façon dont les nombres sont regroupés. Par « groupé », nous entendons « comment vous utilisez les parenthèses ». En d'autres termes, si vous ajoutez ou multipliez, peu importe où vous mettez la parenthèse. Ajoutez des parenthèses où vous le souhaitez
Quelle est l'identité de la multiplication ?

La propriété de multiplication de l'un (également connue sous le nom d'identité multiplicative) indique : a⋅1=a Cela signifie que tout nombre multiplié par 1 restera simplement ce nombre. Multiplier par 1 ne change rien
Quelle est la différence entre propriété inverse et propriété d'identité?

L'axiome d'identité additive stipule qu'un nombre plus zéro est égal à ce nombre. L'axiome multiplicatif de l'identité stipule qu'un nombre multiplié par 1 est ce nombre. L'axiome additif inverse déclare que la somme d'un nombre et l'inverse additif de ce nombre est zéro
