Vidéo: Quelle est la formule de la distribution de probabilité ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Pour calculer cela, nous multiplions chaque valeur possible de la variable par son probabilité , puis ajoutez les résultats. (xje × P(xje)) = {x1 × P(x1)} + {x2 × P(x2)} + {x3 × P(x3)} + E(X) est aussi appelé la moyenne des distribution de probabilité.
Simplement, comment trouvez-vous la distribution de probabilité?
Probabilité . Probabilité est la probabilité qu'un événement se produise et est calculé en divisant le nombre de résultats favorables par le nombre total de résultats possibles. L'exemple le plus simple est un tirage au sort. Lorsque vous lancez une pièce, il n'y a que deux résultats possibles, le résultat est soit pile, soit pile.
Aussi, qu'est-ce qu'une fonction de distribution en probabilité? Les fonction de répartition , également appelé cumul fonction de répartition (CDF) ou fréquence cumulée fonction , Décrit le probabilité qu'une variable prend une valeur inférieure ou égale à un nombre. Les fonction de répartition est parfois aussi noté. (Evans et al. 2000, p. 6).
À cet égard, quelle est la formule de probabilité?
Formule de probabilité est le rapport entre le nombre de résultats favorables et le nombre total de résultats possibles. Mesure la probabilité d'un événement de la manière suivante: - Si P(A) > P(B) alors l'événement A est plus susceptible de se produire que l'événement B. - Si P(A) = P(B) alors les événements A et B sont également susceptibles de se produire.
Quel est un exemple de distribution de probabilité?
Les distribution de probabilité d'une variable aléatoire discrète peut toujours être représentée par un tableau. Pour Exemple , supposons que vous lancez une pièce deux fois. Pour Exemple , les probabilité d'obtenir 1 tête ou moins [P(X < 1)] est P(X = 0) + P(X = 1), ce qui est égal à 0,25 + 0,50 ou 0,75.
Conseillé:
Quelle est la probabilité de l'éruption du Yellowstone ?
En termes de grandes explosions, Yellowstone en a connu trois à 2,08, 1,3 et 0,631 million d'années. Cela correspond à une moyenne d'environ 725 000 ans entre les éruptions. Bien qu'une autre éruption catastrophique à Yellowstone soit possible, les scientifiques ne sont pas convaincus qu'une se produira jamais
Quelle est la courbe de distribution de probabilité radiale ?
La courbe de distribution radiale donne une idée de la densité électronique à une distance radiale du noyau. La valeur de 4πr2ψ2 (fonction de densité de probabilité radiale) devient nulle en un point nodal, également appelé nœud radial. Où n = nombre quantique principal et l = nombre quantique azimutal
Quelle est la moyenne de la distribution du chi carré ?
La distribution du Chi carré est la distribution de la somme des écarts normaux standard au carré. Les degrés de liberté de la distribution sont égaux au nombre d'écarts normaux standard additionnés. La moyenne d'une distribution du Chi carré est ses degrés de liberté
Quelle est la différence entre probabilité conditionnelle et probabilité conjointe ?
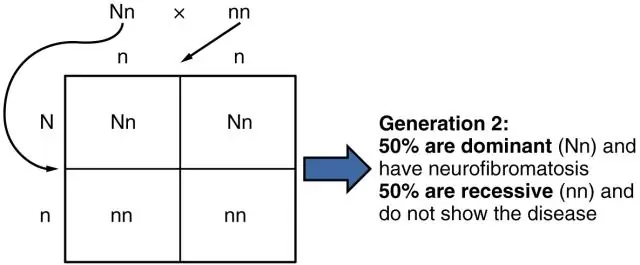
D'une manière générale, la probabilité conjointe est la probabilité que deux choses* se produisent ensemble : par exemple, la probabilité que je lave ma voiture et qu'il pleuve. La probabilité conditionnelle est la probabilité qu'une chose se produise, étant donné que l'autre se produit : par exemple, la probabilité que, étant donné que je lave ma voiture, il pleuve
Qu'est-ce qu'une formule structurelle Quelle est la différence entre une formule structurelle et un modèle moléculaire ?
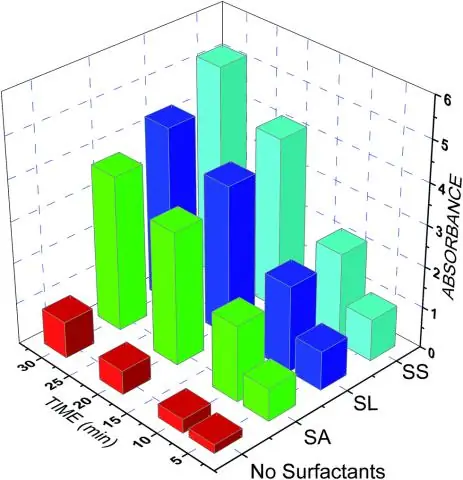
Une formule moléculaire utilise des symboles chimiques et des indices pour indiquer le nombre exact d'atomes différents dans une molécule ou un composé. Une formule empirique donne le rapport en nombre entier le plus simple d'atomes dans un composé. Une formule structurelle indique l'arrangement de liaison des atomes dans la molécule