- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
L'un des avantages de équations paramétriques c'est qu'ils peuvent être utilisé pour représenter graphiquement des courbes qui ne sont pas des fonctions, comme le cercle unité. Un autre avantage de équations paramétriques est que le paramètre peut être utilisé pour représenter quelque chose d'utile et donc nous fournir des informations supplémentaires sur le graphique.
Sachez également, à quoi servent les équations paramétriques ?
Équations paramétriques sont généralement habitué exprimer les coordonnées des points qui composent un objet géométrique tel qu'une courbe ou une surface, auquel cas le équations sont collectivement appelés un paramétrique représentation ou paramétrisation (ou orthographié comme paramétrisation) de l'objet.
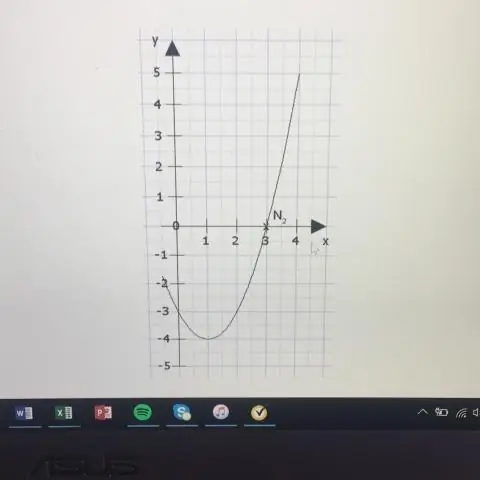
A côté de ci-dessus, comment fonctionnent les équations paramétriques ? Équations paramétriques sont utilisés lorsque x et y ne sont pas directement liés l'un à l'autre, mais sont tous deux liés par un troisième terme. Dans l'exemple, la position de la voiture dans la direction x change linéairement avec le temps, c'est-à-dire que le graphique de sa fonction est une ligne droite.
De plus, qu'entend-on par fonction paramétrique?
Fonctions paramétriques : Définition Fonctions paramétriques sommes les fonctions d'un certain nombre de coordonnées (2 pour le plan à 2 dimensions, 3 pour l'espace à 3 dimensions, et ainsi de suite), où chacune des coordonnées (x, y, z) est exprimée comme une autre fonction d'un paramètre, comme le temps: x = f(t), y = g(t), z = h(t), et ainsi de suite.
Qui a découvert les équations paramétriques ?
Le terme paramétrique tire son origine des mathématiques, mais il y a un débat quant au moment où les concepteurs ont commencé à utiliser le mot. David Gerber (2007, 73), dans sa thèse de doctorat Paramétrique Practice, crédite Maurice Ruiter d'avoir utilisé pour la première fois le terme dans un article de 1988 intitulé Paramétrique Conception [1].
Conseillé:
Pourquoi ajuster les coefficients lors de l'équilibrage des équations chimiques et non des indices ?

Lorsque vous modifiez les coefficients, vous ne modifiez que le nombre de molécules de cette substance particulière. Cependant, lorsque vous modifiez les indices, vous modifiez la substance elle-même, ce qui rendra votre équation chimique erronée
Comment résoudre des équations à plusieurs étapes avec des variables ?

Pour résoudre une équation comme celle-ci, vous devez d'abord obtenir les variables du même côté du signe égal. Ajoutez -2,5y des deux côtés pour que la variable ne reste que d'un côté. Isolez maintenant la variable en soustrayant 10,5 des deux côtés. Multipliez les deux côtés par 10 pour que 0,5y devienne 5y, puis divisez par 5
Que peut-on utiliser pour déterminer la vitesse des réactions catalysées par des enzymes ?

La catalyse enzymatique est détectée en mesurant soit l'apparition de produit, soit la disparition de réactifs. Pour mesurer quelque chose, il faut pouvoir le voir. Les dosages enzymatiques sont des tests développés pour mesurer l'activité enzymatique en mesurant le changement de concentration d'une substance détectable
Quelle est la différence entre des expressions équivalentes et des équations équivalentes ?
Les expressions équivalentes ont la même valeur mais sont présentées dans un format différent en utilisant les propriétés des nombres, par exemple, ax + bx = (a + b)x sont des expressions équivalentes. Strictement, ils ne sont pas « égaux », nous devrions donc utiliser 3 lignes parallèles dans le « égal » plutôt que 2 comme indiqué ici
Quand devez-vous utiliser la corrélation et quand devez-vous utiliser la régression linéaire simple ?

La régression est principalement utilisée pour créer des modèles/équations afin de prédire une réponse clé, Y, à partir d'un ensemble de variables prédictives (X). La corrélation est principalement utilisée pour résumer rapidement et de manière concise la direction et la force des relations entre un ensemble de 2 ou plusieurs variables numériques
