
- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
Résumé: - Le problème du voyageur de commerce ( TSP ) est l'un des problèmes les plus étudiés en mathématiques computationnelles et en optimisation combinatoire. Il est également considéré comme la classe des problèmes d'optimisation combinatoire NP-complet.
Sachez aussi, qu'est-ce que le TSP en informatique ?
Le problème du voyageur de commerce ( TSP ) est un problème analgorithmique chargé de trouver le chemin le plus court entre un ensemble de points et de lieux qui doivent être visités. Axé sur l'optimisation, TSP est souvent utilisé dans l'informatique pour trouver l'itinéraire le plus efficace pour que les données voyagent entre les différents nœuds.
Sachez également que TSP est-il un NP ? Pourquoi TSP N'est pas NP -complet Puisqu'il n'est pas dans NP , ça ne peut pas être NP -Achevée. Dans TSP vous recherchez la boucle la plus courte qui traverse chaque ville dans un ensemble donné de villes. Puisqu'il faut un temps exponentiel pour résoudre NP , la solution ne peut pas être vérifiée en temps polynomial. Ainsi ce problème est NP -dur, mais pas dans NP.
En tenant compte de cela, qu'est-ce que le TSP dans DAA ?
Le problème du voyageur de commerce ( TSP ) est un problème mathématique populaire qui demande la trajectoire la plus efficace possible étant donné un ensemble de points et de distances qui doivent tous être visités. En informatique, le problème peut être appliqué à la route la plus efficace pour que les données voyagent entre divers nœuds.
Pourquoi le TSP NP est-il complet ?
Preuve: pour montrer que TSP est NP - Dur , nous devons montrer que tout problème y dans NP réduit à TSP en temps polynomial. Pour ce faire, considérons la version décisionnelle du cycle hamiltonien (HC). Il est bien connu que HC est NP - Compléter , donc HC est NP - Dur ettous les problèmes y sont NP réduit à HC en temps polynomial.
Conseillé:
Quel est le rôle de CDK dans le fonctionnement normal des cellules, en particulier dans le cycle cellulaire ?

Grâce à la phosphorylation, les Cdks signalent à la cellule qu'elle est prête à passer à l'étape suivante du cycle cellulaire. Comme leur nom l'indique, les protéines kinases dépendantes des cyclines dépendent des cyclines, une autre classe de protéines régulatrices. Les cyclines se lient aux Cdks, activant les Cdks pour phosphoryler d'autres molécules
Selon vous, quel est le rôle de l'ARN dans la fabrication des protéines dans la cellule ?

L'ARN ribosomique (ARNr) s'associe à un ensemble de protéines pour former des ribosomes. Ces structures complexes, qui se déplacent physiquement le long d'une molécule d'ARNm, catalysent l'assemblage d'acides aminés en chaînes protéiques. Ils se lient également aux ARNt et à diverses molécules accessoires nécessaires à la synthèse des protéines
Qu'est-ce que c'est que ce truc d'argent dans un thermomètre ?

Un liquide rouge dans un thermomètre à liquide en verre est composé d'alcools minéraux ou d'alcool éthanol mélangé à un colorant rouge. Un liquide gris ou argenté à l'intérieur du thermomètre est du mercure
Lequel des éléments suivants est présent dans les cellules animales mais pas dans les cellules végétales ?
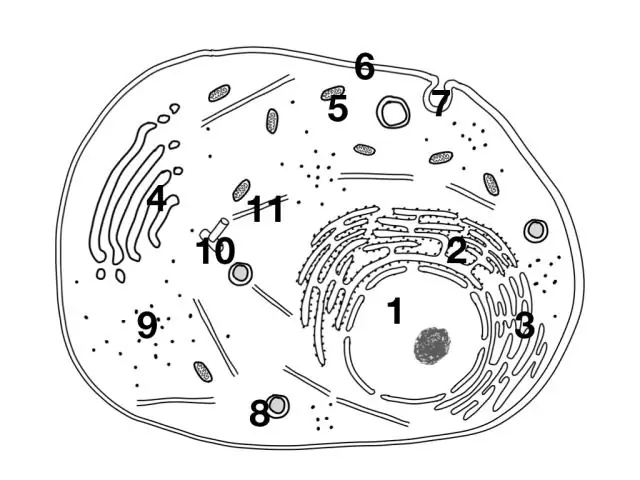
Mitochondries, paroi cellulaire, membrane cellulaire, chloroplastes, cytoplasme, vacuole. La paroi cellulaire, les chloroplastes et la vacuole se trouvent dans les cellules végétales plutôt que dans les cellules animales
Est-ce que des éléments ayant des propriétés chimiques similaires sont plus susceptibles d'être trouvés dans la même période ou dans le même groupe expliquent votre réponse ?

C'est parce que les propriétés chimiques dépendent du nombre d'électrons de valence. Comme dans un groupe, tous les éléments ont le même numéro d'électron de valence, c'est pourquoi ils ont des propriétés chimiques similaires, mais dans une période, le numéro d'électron de valence varie, c'est pourquoi ils diffèrent par leurs propriétés chimiques
