Vidéo: Quelle est la phase avancée du processus de réduction des rangs ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Les positions de pivot dans un matrice sont complètement déterminés par les positions des entrées de tête dans les lignes non nulles de toute forme d'échelon obtenue à partir du matrice . Réduire un matrice à la forme échelonnée est appelée la phase avancée du processus de réduction des rangs.
En conséquence, quel est l'algorithme de réduction de ligne ?
L'élimination de Gauss, également appelée réduction de ligne , est un algorithme en algèbre linéaire pour résoudre un système d'équations linéaires. Il est généralement compris comme une séquence d'opérations effectuées sur la matrice de coefficients correspondante. La méthode porte le nom de Carl Friedrich Gauss (1777-1855).
A côté de ci-dessus, qu'est-ce que les opérations élémentaires sur les lignes des matrices ? Opérations élémentaires Multipliez chaque élément dans un ligne (ou colonne) par un nombre différent de zéro. Multiplier un ligne (ou colonne) par un nombre différent de zéro et ajouter le résultat à un autre ligne (ou colonne).
Sachez également que l'algorithme de réduction de lignes s'applique uniquement aux matrices augmentées ?
Les l'algorithme de réduction de ligne s'applique uniquement aux matrices augmentées pour un système linéaire. Réponse: Faux. Tout la matrice peut être réduit . Si un ligne sous la forme d'un échelon matrice augmentée est [0 0 0 5 0], alors le système linéaire associé est incohérent.
Pouvez-vous Row réduire avant de trouver le déterminant ?
Déterminant d'une matrice triangulaire ou diagonale supérieure (inférieure) est égal au produit de ses entrées diagonales. detA =detAT, donc on pouvez appliquer soit ligne ou des opérations de colonne pour obtenir le déterminant . 2. Si deux Lignes ou deux colonnes de A sont identiques ou si A a un ligne ou une colonne de zéros, alors detA = 0.
Conseillé:
Quelle est la fonction des protéines de la phase aiguë ?
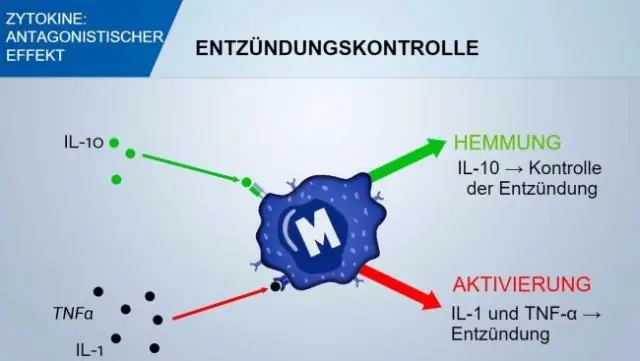
Les protéines de phase aiguë positives remplissent (dans le cadre du système immunitaire inné) différentes fonctions physiologiques au sein du système immunitaire. Certains agissent pour détruire ou inhiber la croissance des microbes, par exemple la protéine C réactive, la protéine de liaison au mannose, les facteurs du complément, la ferritine, la céruloplasmine, l'amyloïde A sérique et l'haptoglobine
Qu'est-ce qu'un processus spontané et un processus non spontané ?
Un processus spontané est un processus qui se produit sans l'intervention de l'extérieur. Un processus non spontané n'aurait pas lieu sans l'intervention de l'extérieur
Quelle phase de la méiose I est la plus similaire à la phase comparable de la mitose ?
Raccourcis clavier pour l'utilisation des cartes mémoire : lequel des éléments suivants n'est pas une caractéristique distincte de la méiose ? fixation des kinétochores sœurs aux microtubules fusiformes quelle phase de la méiose I est la plus similaire à la phase comparable de la mitose ? télophase I
Qu'est-ce que la chromatographie en phase normale et en phase inverse?
En chromatographie en phase normale, la phase stationnaire est polaire et la phase mobile est non polaire. En phase inversée, nous avons tout le contraire; la phase stationnaire est apolaire et la phase mobile est polaire
Quel processus est un processus endothermique ?
Un processus endothermique est tout processus qui nécessite ou absorbe de l'énergie de son environnement, généralement sous forme de chaleur. Il peut s'agir d'un processus chimique, tel que la dissolution du nitrate d'ammonium dans l'eau, ou d'un processus physique, tel que la fonte de glaçons