Vidéo: Comment calcule-t-on l'accélération de rotation ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Accélération angulaire (α) peut être défini comme angulaire vitesse (ω) divisée par accélération temps (t). Alternativement, pi (π) multiplié par la vitesse d'entraînement (n) divisé par accélération temps (t) multiplié par 30. Ce équation donne la norme accélération angulaire Unité SI de radians par seconde au carré (Rad/sec^2).
Simplement, qu'est-ce que la formule d'accélération angulaire?
Accélération angulaire est défini comme le taux de variation de angulaire rapidité. Dans équation former, accélération angulaire s'exprime comme suit: α=ΔωΔt α = Δ ω Δ t, où est la variation de angulaire vitesse et t est le changement dans le temps. Les unités de accélération angulaire sont (rad/s)/s, ou rad/s2.
De même, de quoi dépend l'accélération angulaire ? Dans le mouvement de rotation, un couple est nécessaire pour produire un accélération angulaire d'un objet. La quantité de couple nécessaire pour produire un l'accélération angulaire dépend de la distribution de la masse de l'objet. Le moment d'inertie est une valeur qui décrit la distribution.
À côté de ci-dessus, comment l'accélération peut-elle être calculée ?
Réorganiser l'équation F = ma pour résoudre pour accélération . Vous pouvez modifier cette formule pour résoudre pour accélération en divisant les deux côtés par la masse, donc: a = F/m. Pour trouver le accélération , divisez simplement la force par la masse de l'objet accéléré.
A quoi est égale l'accélération angulaire ?
C'est le changement dans le angulaire vitesse, divisé par le changement dans le temps. La moyenne accélération angulaire est le changement dans le angulaire vitesse, divisé par le changement dans le temps. Les accélération angulaire est un vecteur qui pointe dans une direction le long de l'axe de rotation.
Conseillé:
Comment calcule-t-on la circonférence de la Terre à sa latitude ?
La circonférence d'un cercle est égale à 2πr où r est son rayon. Sur Terre, la circonférence de la sphère à une latitude donnée est de 2πr(cos θ) où θ est la latitude et r est le rayon de la Terre à l'équateur
Comment calcule-t-on la rotation optique ?
Pour une substance optiquement active, définie par [α]θλ = α/γl, où est l'angle à travers lequel la lumière polarisée plane est tournée par une solution de concentration en masse γ et la longueur du chemin l. Ici θ est la température Celsius et λ la longueur d'onde de la lumière à laquelle la mesure est effectuée
Quelle est la formule pour calculer la rotation spécifique à partir de la rotation observée ?
Pour convertir une rotation observée en rotation spécifique, divisez la rotation observée par la concentration en g/mL et la longueur du trajet optique en décimètres (dm)
Comment calcule-t-on l'énergie cinétique de rotation ?
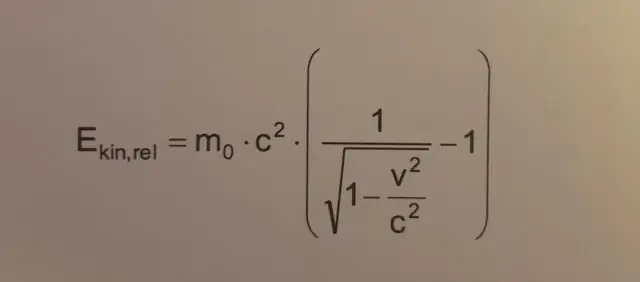
L'énergie cinétique rotationnelle peut être exprimée comme suit : Érotationnel=12Iω2 E rotationnel = 1 2 I ω 2 où ω est la vitesse angulaire et I est le moment d'inertie autour de l'axe de rotation. Le travail mécanique appliqué pendant la rotation est le couple multiplié par l'angle de rotation : W=τθ W = τ θ
La rotation optique et la rotation spécifique sont-elles identiques ?
En chimie, la rotation spécifique ([α]) est une propriété d'un composé chimique chiral. Si un composé est capable de faire tourner le plan de polarisation de la lumière polarisée dans le plan, il est dit « optiquement actif ». La rotation spécifique est une propriété intensive, la distinguant du phénomène plus général de rotation optique