Table des matières:
Vidéo: Quelles sont les hypothèses de la programmation linéaire ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Hypothèses de la programmation linéaire
- Conditions de certitude. Cela signifie que les nombres dans le objectif et les contraintes sont connues avec certitude et évoluent au cours de la période étudiée.
- Linéarité ou proportionnalité.
- Additivement.
- Divisibilité.
- Variable non négative.
- Finitude.
- Optimalité.
Par la suite, on peut également se demander, laquelle des hypothèses suivantes est une hypothèse de base de la programmation linéaire ?
La condition d'incertitude existe. L'indépendance existe pour les activités. La proportionnalité existe dans la fonction objective et les contraintes.
quels sont les composants de la programmation linéaire ? Il se compose de quatre bases Composants : Les variables de décision représentent des quantités à déterminer. La fonction objectif représente comment les variables de décision affectent le coût ou la valeur à optimiser (minimisé ou maximisé)
En gardant cela à l'esprit, quelles sont les hypothèses et les limites de la programmation linéaire ?
Hypothèses et limites de la programmation linéaire
- Il existe un certain nombre de restrictions ou de contraintes exprimables en termes quantitatifs.
- Les paramètres sont sujets à des variations de grandeur.
- Les relations exprimées par les contraintes et les fonctions objectifs sont linéaires.
- La fonction objectif doit être optimisée par rapport à les variables impliquées dans le phénomène.
Qu'est-ce que la divisibilité en programmation linéaire ?
Divisibilité - les variables de décision peuvent être divisées en valeurs non entières, prenant des valeurs fractionnaires. Entier la programmation techniques peuvent être utilisées si le divisibilité l'hypothèse ne tient pas.
Conseillé:
Quelles sont les hypothèses de base de la psychologie évolutionniste ?
Quelles sont les hypothèses de base de la psychologie évolutionniste ? 1. Toutes les caractéristiques influencées par l'évolution se développent. 3. Le développement est limité par des facteurs génétiques, environnementaux et culturels
Quelles sont les hypothèses qui sous-tendent la méthode de Lincoln Petersen ?
Hypothèses fondamentales de l'estimateur Lincoln-Petersen : La population est fermée (géographiquement et démographiquement). Tous les animaux sont également susceptibles d'être capturés dans chaque échantillon. La capture et le marquage n'affectent pas la capturabilité
Qu'est-ce que la régression linéaire en programmation R ?
La régression linéaire est utilisée pour prédire la valeur d'une variable continue Y basée sur une ou plusieurs variables prédictives d'entrée X. L'objectif est d'établir une formule mathématique entre la variable de réponse (Y) et les variables prédictives (Xs). Vous pouvez utiliser cette formule pour prédire Y, lorsque seules les valeurs X sont connues
Quelles sont les hypothèses de base de la théorie cinétique des gaz ?
Le modèle cinétique le plus simple repose sur les hypothèses suivantes : (1) le gaz est composé d'un grand nombre de molécules identiques se déplaçant dans des directions aléatoires, séparées par des distances importantes par rapport à leur taille; (2) les molécules subissent des collisions parfaitement élastiques (pas de perte d'énergie) entre elles et avec le
Quelle est la méthode du simplexe pour la programmation linéaire?
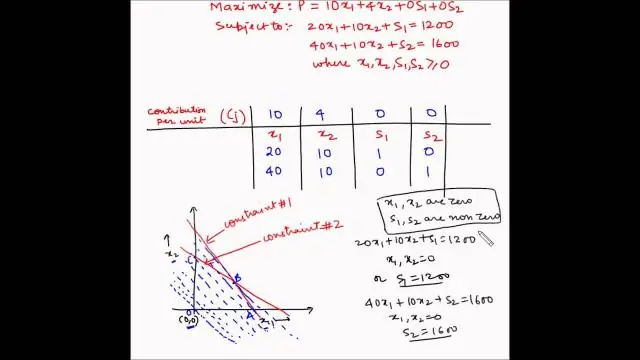
Méthode simplex. Méthode simplex, technique standard en programmation linéaire pour résoudre un problème d'optimisation, généralement impliquant une fonction et plusieurs contraintes exprimées sous forme d'inégalités. Les inégalités définissent une région polygonale (voir polygone), et la solution est généralement à l'un des sommets