Vidéo: Comment faites-vous des événements composés de probabilité?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
Déterminer le probabilité d'un événement composé consiste à trouver la somme des probabilités de l'individu événements et, si nécessaire, supprimer tout chevauchement probabilités . Une exclusivité événement composé est celui dans lequel le multiple les événements font pas se chevaucher. En termes mathématiques: P(C) = P(A) + P(B).
De même, les gens demandent, comment trouvez-vous la probabilité expérimentale d'un événement composé ?
À trouve les probabilité de l'un ou de l'autre mutuellement inclus un événement , ajoutez l'individu probabilités et soustraire le probabilité ils se produisent en même temps.
On peut aussi se demander, qu'est-ce qu'un événement composite en probabilité ? UNE événement composite est un un événement constitué d'un groupement d'élèves élémentaires événements , les résultats possibles des trois pièces jetées ensemble sont un événement composite . Les un événement est le résultat possible d'un un événement . Il peut avoir les valeurs suivantes: (1) Un seul élément: Reine de Cœur d'un jeu de cartes: {Q }
Justement, comment trouvez-vous la probabilité d'un événement?
Les probabilité d'un événement est le nombre de résultats favorables divisé par le nombre total de résultats possibles. En convertissant la fraction 35 en un nombre décimal, nous dirions qu'il y a 0,6 probabilité de choisir une banane. Cette définition de base de probabilité suppose que tous les résultats sont également susceptibles de se produire.
Comment trouve-t-on la probabilité de 3 événements ?
Union de trois événements (formule d'inclusion/exclusion): P(A B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(A ∩ C) − P(B ∩ C) + P(A B C). Dessinez des diagrammes de Venn: les diagrammes de Venn vous aident à imaginer ce qui se passe et à déduire les probabilités.
Conseillé:
Comment une protéine à l'extérieur de la cellule peut-elle provoquer des événements à l'intérieur de la cellule ?
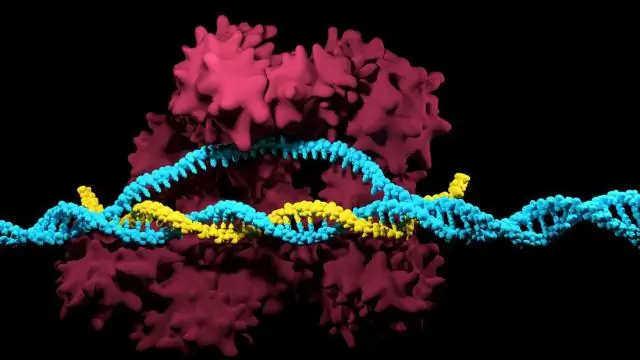
Une protéine peut traverser la membrane et pénétrer dans la cellule, provoquant une signalisation à l'intérieur de la cellule. b. Une protéine à l'extérieur de la cellule peut se lier à une protéine réceptrice à la surface de la cellule, la faisant changer de forme et envoyant un signal à l'intérieur de la cellule. La phosphorylation modifie la forme de la protéine, l'activant le plus souvent
Qu'est-ce que la probabilité d'événements indépendants ?
En probabilité, deux événements sont indépendants si l'incidence d'un événement n'affecte pas la probabilité de l'autre événement. Si l'incidence d'un événement affecte la probabilité de l'autre événement, alors les événements sont dépendants. Il y a un dé équitable rouge à 6 faces et un dé équitable bleu à 6 faces
Que sont les composés organiques et les composés inorganiques ?
La principale différence réside dans la présence d'un atome de carbone; les composés organiques contiendront un atome de carbone (et souvent un atome d'hydrogène, pour former des hydrocarbures), alors que presque tous les composés inorganiques ne contiennent aucun de ces deux atomes. Pendant ce temps, les composés inorganiques comprennent les sels, les métaux et autres composés élémentaires
Quelle est la différence entre probabilité conditionnelle et probabilité conjointe ?
D'une manière générale, la probabilité conjointe est la probabilité que deux choses* se produisent ensemble : par exemple, la probabilité que je lave ma voiture et qu'il pleuve. La probabilité conditionnelle est la probabilité qu'une chose se produise, étant donné que l'autre se produit : par exemple, la probabilité que, étant donné que je lave ma voiture, il pleuve
Pourquoi les écologistes posent-ils des questions sur les événements et les organismes qui s'étendent ?
Pourquoi les écologistes posent-ils des questions sur des événements et des organismes dont la complexité va d'un individu à la biosphère ? Pour comprendre les relations au sein de la biosphère, les écologistes posent des questions sur des événements et des organismes dont la complexité va d'un seul individu à l'ensemble de la biosphère