
- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- Dernière modifié 2025-01-22 16:58.
Réponse et explication:
Les racine carrée de infini est infini . Si vous choisissez un nombre et le multipliez par lui-même, vous auriez au carré le nombre.
De même, on peut se demander, qu'est-ce que le carré de l'infini ?
Les carré de l'infini peut être exprimé comme la limite suivante. limx→∞√x=+∞ d'où le carré racine de infini est infini . Aussi, nous savons que ∞⋅∞=∞ donc nous concluons la même réponse. La limite de la carré la racine de zéro est zéro.
Par la suite, la question est: la racine carrée de 2 est-elle infinie ? Parce que 2 n'est pas un entier ( 2 n'est pas parfait carré ), √ 2 doit donc être irrationnel. Voir quadratique irrationnel ou infini descente pour une preuve que le racine carrée de tout non- carré l'entier naturel est irrationnel.
Ici, qu'est-ce que l'infini divisé par l'infini ?
Cependant, 1 divisé par ∞ est égal à une limite approchant 0. En d'autres termes, 1 divisé par n'est pas égal à un nombre ou n'est pas défini. En conséquence, nous sommes arrivés à une impasse. Par conséquent, l'infini divisé par l'infini est encore indéfini.
L'infini au carré est-il plus grand que l'infini ?
Donc infini élevé au pouvoir de infini serait plus grand que "ordinaire infini . " Mais l'infini au carré , inf * inf, correspond au nombre de nombres rationnels. Donc infini élevé au pouvoir de infini serait plus grand que "ordinaire infini .”
Conseillé:
La racine carrée 3 est-elle un entier ?

Racine carrée de &moins;3. (voir racine carrée des nombres négatifs). C'est un entier d'Eisenstein. À savoir, il est exprimé comme la différence entre deux racines cubiques non réelles de 1 (qui sont des entiers d'Eisenstein)
La racine carrée de 9 31 est-elle un nombre irrationnel ?

Réponse : Non, 9/31 n'est pas un nombre irrationnel. Où p et q sont tous deux des nombres entiers et q ≠ 0, sinon, il est appelé nombre irrationnel
Pourquoi y racine carrée de x n'est-elle pas une fonction ?
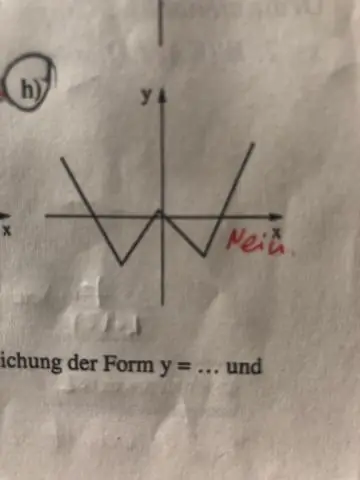
Y=x² peut être résolu pour x en prenant la racine carrée des deux côtés. La racine carrée d'un nombre donne à la fois une réponse positive. x=±√y n'est pas une fonction car pour certaines entrées x (ou dans ce cas presque toutes les entrées x), il y a deux sorties y différentes
Qu'est-ce que l'extraction de la racine carrée ?

L'extraction des racines consiste à isoler le carré, puis à appliquer la propriété racine carrée. N'oubliez pas d'inclure « ± » lorsque vous prenez la racine carrée des deux côtés. Après avoir appliqué la propriété racine carrée, résolvez chacune des équations résultantes
Peut-on multiplier une racine cubique par une racine carrée ?

Le produit élevé à une règle de puissance est important car vous pouvez l'utiliser pour multiplier des expressions radicales. Notez que les racines sont les mêmes : vous pouvez combiner des racines carrées avec des racines carrées ou des racines cubiques avec des racines cubiques, par exemple. Mais vous ne pouvez pas multiplier une racine carrée et une racine cubique en utilisant cette règle
