Table des matières:
Vidéo: Quelle preuve utilise des chiffres sur un plan de coordonnées pour prouver des propriétés géométriques ?
2024 Auteur: Miles Stephen | [email protected]. Dernière modifié: 2023-12-15 23:36
UNE preuve cette utilise des chiffres sur un plan de coordonnées pour prouver les propriétés géométriques est dite trigonométrique.
Sachez également, qu'est-ce qu'une preuve de coordonnées en géométrie?
Les preuve de coordonnées est un preuve d'un géométrique théorème qui utilise des points "généralisés" sur le plan cartésien pour faire un argument. La méthode consiste généralement à affecter des variables aux coordonnées d'un ou plusieurs points, puis en utilisant ces variables dans les formules de point médian ou de distance.
On peut aussi se demander, quelle preuve utilise des chiffres ? UNE preuve cette utilise des chiffres sur un plan de coordonnées à prouver propriétés géométriques est appelée trigonométrique.
Sachez également, qu'est-ce qu'un exemple de preuve de coordonnées?
Dans un preuve de coordonnées , vous prouvez des énoncés géométriques en utilisant l'algèbre et le coordonner avion. Certains exemples des déclarations que vous pourriez prouver avec un preuve de coordonnées sont: Prouver ou réfuter que le quadrilatère défini par les points egin{align*}(2, 4), (1, 2), (5, 1), (4, -1)end{align*} est un parallélogramme.
Comment prouver un triangle isocèle sur un graphique ?
Étapes pour coordonner la preuve
- tracer les 3 points (facultatif)
- utiliser la formule de distance pour calculer la longueur de côté de chaque côté du triangle.
- Si 2 côtés ont des longueurs de côté égales, alors le triangle est isocèle.
Conseillé:
Comment trouver le facteur d'échelle d'une dilatation sur un plan de coordonnées ?
Représentez graphiquement le triangle ABC avec les coordonnées A(2, 6), B(2, 2), C(6, 2). Ensuite, dilatez l'image par un facteur d'échelle de 1/2 avec l'origine comme centre de dilatation. Tout d'abord, nous représentons graphiquement notre triangle d'origine dans le plan de coordonnées. Ensuite, nous multiplions chaque coordonnée par le facteur d'échelle de 1/2
Comment représenter graphiquement des inégalités sur un plan de coordonnées ?
Il y a trois étapes : Réorganisez l'équation de sorte que « y » soit à gauche et tout le reste à droite. Tracez la ligne 'y=' (faites-en une ligne continue pour y≤ ou y≥, et une ligne pointillée pour y) Ombrez au-dessus de la ligne pour un 'supérieur à' (y> ou y≥) ou en dessous de la ligne pour un 'inférieur à' (y< ou y≤)
Comment prouver un cerf-volant en géométrie de coordonnées?
Voici les deux méthodes : Si deux paires disjointes de côtés consécutifs d'un quadrilatère sont congruentes, alors c'est un cerf-volant (inverse de la définition du cerf-volant). Si l'une des diagonales d'un quadrilatère est la médiatrice de l'autre, alors c'est un cerf-volant (inverse d'une propriété)
Lesquelles des propriétés suivantes sont toutes des propriétés physiques de la matière ?
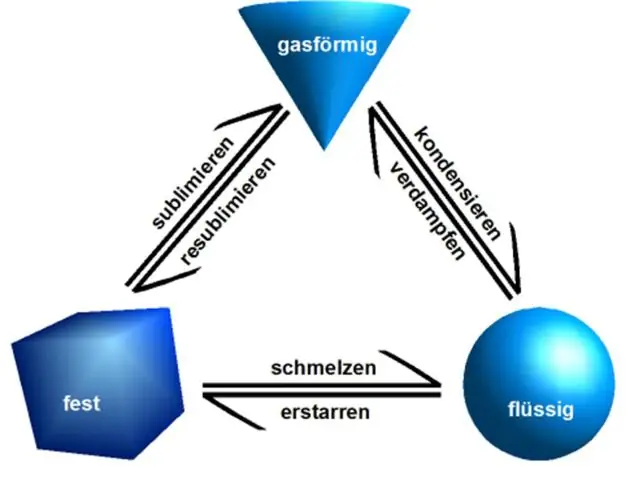
Propriétés physiques : Les propriétés physiques peuvent être observées ou mesurées sans modifier la composition de la matière. Les propriétés physiques comprennent : l'apparence, la texture, la couleur, l'odeur, le point de fusion, le point d'ébullition, la densité, la solubilité, la polarité et bien d'autres
Que sont les entiers et les nombres rationnels Comment les points sont-ils représentés graphiquement sur un plan de coordonnées ?
Comme nous l'avons dit, les points sur le plan de coordonnées sont représentés par (a, b), où a et b sont des nombres rationnels. Les nombres rationnels sont des nombres qui peuvent être écrits sous forme de fraction, p/q, où p et q sont des nombres entiers. Nous appelons a la coordonnée x du point et nous appelons b la coordonnée y du point